Question

13．第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行．下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）．

	第30届伦敦	第29届北京	第28届雅典	第27届悉尼	第26届亚特兰大
中国	38	51	32	28	16
俄罗斯	24	23	27	32	26

（Ⅰ）根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；
（Ⅱ）下表是近五届奥运会中国代表团获得的金牌数之和y（从第26届算起，不包括之前已获得的金牌数）随时间x变化的数据：

时间x（届）	26	27	28	29	30
金牌数之和y（枚）	16	44	76	127	165

作出散点图如图1：

（i）由图可以看出，金牌数之和y与时间x之间存在线性相关关系，请求出y关于x的线性回归方程；
（ii）利用（i）中的回归方程，预测今年中国代表团获得的金牌数．
参考数据：$\overline{x}$=28，$\overline{y}$=85.6，$\sum_{i=1}^{n}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）=381，$\sum_{i=1}^{n}$（x_i-$\overline{x}$）²=10
附：对于一组数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n），其回归直线y=bx+a的斜率和截距的最小二乘估计分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．

Answer 1

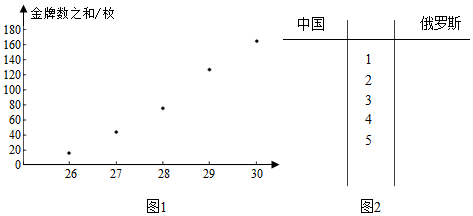
分析 （Ⅰ）根据题意，画出茎叶图，通过茎叶图得出概率结论；
（Ⅱ）（i）计算线性回归方程的系数$\stackrel{∧}{b}$、$\stackrel{∧}{a}$，写出线性回归方程，
（ii）利用回归方程计算x=31时$\stackrel{∧}{y}$的值即可．

解答 解：（Ⅰ）两国代表团获得的金牌数的茎叶图如下，…（3分）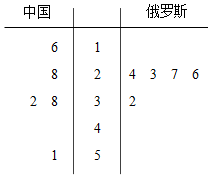

通过茎叶图可以看出，
中国代表团获得的金牌数的平均值高于俄罗斯代表团获得的金牌数的平均值；
俄罗斯代表团获得的金牌数比较集中，中国代表团获得的金牌数比较分散；…（6分）
（Ⅱ）（i）计算$\stackrel{∧}{b}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}{（x}_{i}-\overline{x}）{（y}_{i}-\overline{y}）}{{\underset{\stackrel{n}{∑}}{i=1}{（x}_{i}-\overline{x}）}^{2}}$=$\frac{381}{10}$=38.1，
所以$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=85.6-38.1×28=-981.2；
所以金牌数之和y关于时间x的线性回归方程为$\stackrel{∧}{y}$=38.1x-981.2； …（9分）
（ii）由（i）知，当x=31时，中国代表团获得的金牌数之和的预报值
$\stackrel{∧}{y}$=38.1×31-981.2=199.9，
故预测今年中国代表团获得的金牌数为199-165=34.9≈35枚．…（12分）

点评 本题考查了线性回归方程的应用问题，也考查了茎叶图的应用问题，是基础题目．