
分析 (1)由已知a3,a4,a5成等差数列,a2,a3,a4成等比数列,a1,a2,a3成等差数列,由此能求出a1.
(2)由已知得2a2n=a2n-1+a2n+1,${{a}_{2n+1}}^{2}={{a}_{2n+2}•{a}_{2n}}^{\;}$,${{a}_{2n-1}}^{2}={a}_{2n-2}{a}_{2n}$,n≥2,由此能证明数列{$\sqrt{{a}_{2n}}$}是等差数列.
(3)由数列{$\sqrt{{a}_{2n}}$}是等差数列,推导出a2n=$\frac{[({a}_{2}-{a}_{1})n+{a}_{1}]^{2}}{{a}_{2}}$,由此根据当n=2m,m∈N*和当n=2m-1,m∈N*,m≥2两种情况分类讨论,能证明对任意n∈N*,且n≥2,都有$\frac{{a}_{n+1}}{{a}_{n}}$$<\frac{{a}_{2}}{{a}_{1}}$.
解答 解:(1)∵数列{an}满足对任意n∈N*,an>0,a2n-1,a2n,a2n+1成等差数列,
∴a3,a4,a5成等差数列,设公差为d,则a3=3-2d,a4=3-d.
∵a2n,a2n+1,a2n+2成等比数列,∴a2,a3,a4成等比数列,
∴${a}_{2}=\frac{{{a}_{3}}^{2}}{{a}_{4}}$=$\frac{(3-2d)^{2}}{3-d}$,
∵a2=1,∴$\frac{(3-2d)^{2}}{3-d}=1$,解得d=2或d=$\frac{3}{4}$,∵an>0,∴d=$\frac{3}{4}$,
∵a1,a2,a3成等差数列,
∴a1=2a2-a3=2-(3-2d)=$\frac{1}{2}$.
证明:(2)∵a2n-1,a2n,a2n+1成等差数列,a2n,a2n+1,a2n+2成等比数列,
∴2a2n=a2n-1+a2n+1,${{a}_{2n+1}}^{2}={{a}_{2n+2}•{a}_{2n}}^{\;}$,
∴${{a}_{2n-1}}^{2}={a}_{2n-2}{a}_{2n}$,n≥2,
∴$\sqrt{{a}_{2n-2}{a}_{2n}}$+$\sqrt{{a}_{2n}{a}_{2n+2}}$=2a2n,
∵an>0,∴$\sqrt{{a}_{2n-2}}+\sqrt{{a}_{2n+2}}$=2$\sqrt{{a}_{2n}}$,
∴数列{$\sqrt{{a}_{2n}}$}是等差数列.
(3)∵数列{$\sqrt{{a}_{2n}}$}是等差数列,∴$\sqrt{{a}_{2n}}$=$\sqrt{{a}_{2}}+(n-1)(\sqrt{{a}_{1}}-\sqrt{{a}_{2}})$,
∵a1,a2及a2n,a2n+1,a2n+2成等比数列,a2n-1,a2n,a2n+1成等差数列,
∴${a}_{1}=\frac{(2{a}_{2}-{a}_{1})^{2}}{{a}_{2}}$,
∴$\sqrt{{a}_{2n}}=\sqrt{{a}_{2}}+(n-1)(\sqrt{{a}_{1}}-\sqrt{{a}_{2}})$=$\frac{({a}_{2}-{a}_{1})n+{a}_{1}}{\sqrt{{a}_{2}}}$,
∴a2n=$\frac{[({a}_{2}-{a}_{1})n+{a}_{1}]^{2}}{{a}_{2}}$,
∴${a}_{2n+2}=\frac{[({a}_{2}-{a}_{1})(n+1)+{{a}_{1}}^{2}]}{{a}_{2}}$,
从而${a}_{2n+1}=\sqrt{{a}_{2n}{a}_{2n+2}}$=$\frac{[({a}_{2}-{a}_{1})n+{a}_{1}][({a}_{2}-{a}_{1})(n+1)+{a}_{1}]}{{a}_{2}}$,
∴${a}_{2n-1}=\frac{[({a}_{2}-{a}_{1})(n-1)+{a}_{1}][({a}_{2}-{a}_{1})n+{a}_{1}]}{{a}_{2}}$,
①当n=2m,m∈N*时,
$\frac{{a}_{n+1}}{{a}_{n}}-\frac{{a}_{2}}{{a}_{1}}$=$\frac{\frac{[({a}_{2}-{a}_{1})m+{a}_{1}][({a}_{2}-{a}_{1})(m+1)+{a}_{1}]}{{a}_{2}}}{\frac{[({a}_{2}-{a}_{1})m+{a}_{1}]^{2}}{{a}_{2}}}$-$\frac{{a}_{2}}{{a}_{1}}$
=$\frac{({a}_{2}-{a}_{1})(m+1)+{a}_{1}}{({a}_{2}-{a}_{1})m+{a}_{1}}$-$\frac{{a}_{2}}{{a}_{1}}$
=-$\frac{m({a}_{1}-{a}_{2})^{2}}{{a}_{1}[({a}_{2}-{a}_{1})m+{a}_{1}]}$<0.
②当n=2m-1,m∈N*,m≥2时,
$\frac{{a}_{n+1}}{{a}_{n}}$-$\frac{{a}_{2}}{{a}_{1}}$=$\frac{\frac{[({a}_{2}-{a}_{1})m+{a}_{1}]^{2}}{{a}_{2}}}{\frac{[({a}_{2}-{a}_{1})(m-1)+{a}_{1}][({a}_{2}-{a}_{1})m+{a}_{1}]}{{a}_{2}}}$-$\frac{{a}_{2}}{{a}_{1}}$
=$\frac{({a}_{2}-{a}_{1})m+{a}_{1}}{({a}_{2}-{a}_{1})(m-1)+{a}_{1}}-\frac{{a}_{2}}{{a}_{1}}$
=-$\frac{(m-1_({a}_{1}-{a}_{2})^{2}}{{a}_{1}[({a}_{2}-{a}_{1})(m-1)+{a}_{1}]}$<0.
综上,对任意n∈N*,且n≥2,都有$\frac{{a}_{n+1}}{{a}_{n}}$$<\frac{{a}_{2}}{{a}_{1}}$.
点评 本题考查数列的首项的求法,考查等差数列的证明,考查不等式的证明,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 11 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
| 时间x(届) | 26 | 27 | 28 | 29 | 30 |
| 金牌数之和y(枚) | 16 | 44 | 76 | 127 | 165 |
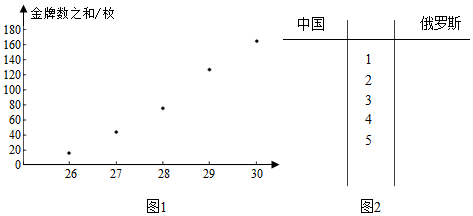
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com