
分析 (1)利用抛物线的定义,可以求出p,即可得到抛物线的方程;
(2)首先设出A,B,C点的坐标,再设出直线AB与y轴交于点D(0,yD),进一步求出yD,根据几何位置关系表示出三角形的面积,再根据基本不等式求出最值及最值成立的条件,则答案可求.
解答 解:(1)由题意知$\frac{p}{2}=1$,即p=2,
∴抛物线C的方程为:x2=4y;
(2)令$A({x_1},\frac{x_1^2}{4}),B({x_2},\frac{x_2^2}{4}),C({x_3},\frac{x_3^2}{4})$,不妨设直线AB与y轴交于点D(0,yD),
∴$\frac{\frac{{{x}_{2}}^{2}}{4}-\frac{{{x}_{1}}^{2}}{4}}{{x}_{2}-{x}_{1}}=\frac{{y}_{D}-\frac{{{x}_{1}}^{2}}{4}}{0-{x}_{1}}$即${y}_{D}=-\frac{{x}_{1}{x}_{2}}{4}$.
又∵且$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴$\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}=0$,$\frac{\frac{{{x}_{1}}^{2}}{4}+\frac{{{x}_{2}}^{2}}{4}+\frac{{{x}_{3}}^{2}}{4}}{3}=1$.
从而x1+x2=-x3,${{x}_{1}}^{2}+{{x}_{2}}^{2}=12-{{x}_{3}}^{2}$
∴$2{x}_{1}{x}_{2}=({x}_{1}+{x}_{2})^{2}-({{x}_{1}}^{2}+{{x}_{2}}^{2})$=$2{{x}_{3}}^{2}-12$,即${x}_{1}{x}_{2}={{x}_{3}}^{2}-6$.
${S_{△ABC}}=3{S_{△ABF}}=3×\frac{1}{2}|{1-{y_D}}||{{x_2}-{x_1}}|$,
$S_{△ABC}^2=\frac{9}{4}{(1+\frac{{{x_1}{x_2}}}{4})^2}(x_1^2+x_2^2-2{x_1}{x_2})=\frac{9}{64}{(4+x_3^2-6)^2}(12-x_3^2-2x_3^2+12)$
=$\frac{9}{64}{(x_3^2-2)^2}(24-3x_3^2)=\frac{27}{64}{(x_3^2-2)^2}(8-x_3^2)$.
令$t=x_3^2≥0$,$y=\frac{27}{64}{(t-2)^2}(8-t)$,${y}^{′}=\frac{27}{64}[2(t-2)(8-t)-(t-2)^{2}]$,令y′=0,则t1=2,t2=6.
当t∈(0,2)时函数单调递减,当t∈(2,6)时函数单调递增,t∈(6,+∞)时函数单调递减且当t=0时y=$\frac{27}{2}$,当t=6时y=$\frac{27}{2}$,
∴${y}_{max}=\frac{27}{2}$.
${S}_{△ABCmax}=\frac{3\sqrt{6}}{2}$.
点评 本题考查了抛物线的标准方程,考查了利用基本不等式求出最值及最值成立的条件,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 11 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
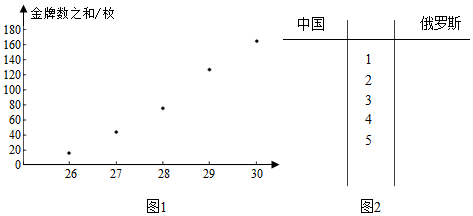
| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
| 时间x(届) | 26 | 27 | 28 | 29 | 30 |
| 金牌数之和y(枚) | 16 | 44 | 76 | 127 | 165 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
| A. | 82 | B. | 84 | C. | 86 | D. | 88 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
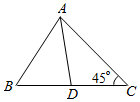 如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°.
如图,在△ABC中,点D在边BC上,BD=2,BA=3,AD=$\sqrt{7}$,∠C=45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
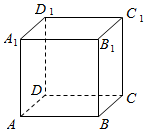 正方体ABCD-A1B1C1D1中,E为A1A的三等分点,F为C1C的三等分点,AE=2A1E,CF=2C1F,过B,E,F作正方体的截面,画出截面在面ACC1A1上的正投影图.
正方体ABCD-A1B1C1D1中,E为A1A的三等分点,F为C1C的三等分点,AE=2A1E,CF=2C1F,过B,E,F作正方体的截面,画出截面在面ACC1A1上的正投影图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com