

分析 (I)由题意知:AE⊥BD,EF⊥BD,根据线面垂直的判定定理得:BD⊥平面AEF,由此能证明平面AEF⊥平面BCD.
(II)过点E作EN∥CD交BC于点N,再过点N作NM∥AC交AF于点M,推导出平面ENM∥平面ACD,从而EM∥平面ACD,由此能求出存在线段AF上满足条件的点M,使得EM∥平面ADC,点M位于线段AF的四等分点处,且AM=3FM.
解答 证明:(I)由题意知:AE⊥BD,EF⊥BD,
而AE∩EF=E,AE,EF?平面AEF,
故根据线面垂直的判定定理可得:BD⊥平面AEF,
又BD?平面BCD,故有平面AEF⊥平面BCD.
解:(II)线段AF上存在满足条件的点M使得EM∥平面ADC,理由如下:
过点E作EN∥CD交BC于点N,再过点N作NM∥AC交AF于点M,
而EN∩NM=N,AC∩CD=C.EN,NM?平面ENM,AC,CD?平面ACD,
故有平面ENM∥平面ACD,
又EM?平面ENM,故EM∥平面ACD,
由题意知点F为线段BC的三等分点,且$FC=2BF=\frac{2}{3}BC$,
而点N为线段BC的中点,$CN=BN=\frac{1}{2}BC$,
于是$FN=FC-NC=\frac{1}{2}BC-\frac{1}{3}BC=\frac{1}{6}BC$,
可得点N为线段CF的四等分点,且CN=3FN,
从而点M为线段AF的四等分点,且AM=3FM,
因此,存在线段AF上满足条件的点M,使得EM∥平面ADC,
点M位于线段AF的四等分点处,且AM=3FM.
点评 本题考查面面垂直的证明,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
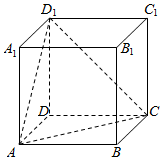 如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )
如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
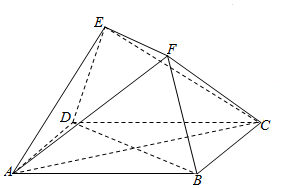 如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.
如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com