
【题目】如果函数f(x)=(x﹣1)2+1定义在区间[t,t+1]上,求f(x)的最小值.
【答案】解:函数f(x)=(x﹣1)2+1对称轴方程为x=1,
顶点坐标为(1,1),图象开口向上,
若顶点横坐标在区间[t,t+1]左侧时,
有1<t,此时,当x=t时,函数取得最小值 ![]() .
.
若顶点横坐标在区间[t,t+1]上时,
有t≤1≤t+1,即0≤t≤1.当x=1时,函数取得最小值f(x)min=f(1)=1.
若顶点横坐标在区间[t,t+1]右侧时,
有t+1<1,即t<0.当x=t+1时,函数取得最小值 ![]()
综上讨论, 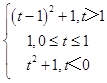
【解析】根据二次函数的大小求出函数的对称轴,通过讨论t的范围,求出函数的最小值即可.
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x||x+1|<1},B={x|y= ![]() ,y∈R},则A∩RB=( )
,y∈R},则A∩RB=( )
A.(﹣2,1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx,g(x)= ![]() .
.
(1)求函数g(x)= ![]() 的单调区间;
的单调区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2sin(x﹣
)+2sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() ).
).
(1)求函数f(x)的最小正周期和图象的对称轴方程.
(2)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,其坐标分别是
,从每条曲线上各取两个点,其坐标分别是![]() ,
, ![]() ,
, ![]() ,
, 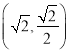 .
.
(1)求![]() ,
, ![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交于不同的两点
交于不同的两点![]() 且满足
且满足![]() ?若存在,求出直线方程;若不存在,请说明理由.
?若存在,求出直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)满足:对任意x1 , x2∈R,当且仅当x1=x2时,有f(x1)=f(x2).则f(﹣1)+f(0)+f(1)的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com