
(本题14分)已知定义域为R的函数 是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的
是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的 ,不等式
,不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;
20.(14分)解:(1)因为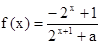 是奇函数
是奇函数
所以f(1)= -f(-1)知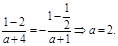 ………………2分
………………2分
(2)解:由(1)知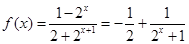 ,
,
设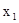 ,
,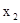
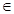 R,且
R,且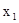 <
<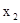
f(x1)-f(x2)=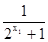 —
—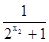 =
=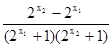 ……………………4分
……………………4分
因为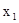 <
<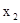 ,
,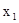 ,
,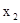
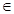 R,
R,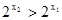 ,
,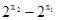 >0 且
>0 且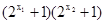 >0………6分
>0………6分
所以f(x1)-f(x2)>0, f(x1)>f(x2)
由单调性定义可知,f(x)在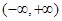 上为减函数。……………………7分
上为减函数。……………………7分
(3)因f(x)是奇函数,从而不等式:
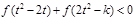 等价于
等价于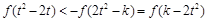 ,………………………8分
,………………………8分
又因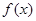 为减函数,由上式推得:
为减函数,由上式推得: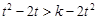 .…………………………10分
.…………………………10分
即对一切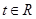 有:
有: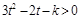 ,
,
从而判别式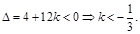 ………………………14分
………………………14分
法二:由(Ⅰ)知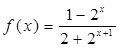 .又由题设条件得:
.又由题设条件得: 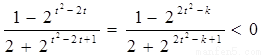 ,
,
即 :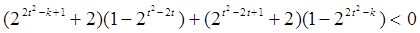 ,
,
整理得 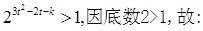
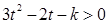 上式对一切
上式对一切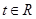 均成立,从而判别式
均成立,从而判别式
【解析】略


科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考文数 题型:解答题
(本题14分)
已知向量 动点
动点 到定直线
到定直线 的距离等于
的距离等于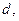 并且满足
并且满足 其中O是坐标原点,
其中O是坐标原点, 是参数.
是参数.
(I)求动点 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(Ⅱ) 当 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(Ⅲ) 如果动点M的轨迹是圆锥曲线,其离心率 满足
满足 求实数
求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)
已知向量![]() 动点
动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() 并且满足
并且满足![]() 其中O是坐标原点,
其中O是坐标原点,![]() 是参数.
是参数.
(I)求动点![]() 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(Ⅱ) 当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(Ⅲ) 如果动点M的轨迹是圆锥曲线,其离心率![]() 满足
满足![]() 求实数
求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)已知椭圆的两个焦点![]() ,且椭圆短轴的
,且椭圆短轴的
两个端点与![]() 构成正三角形.
构成正三角形.
(1)求椭圆的方程;
(2)过点(1,0)且与坐标轴不平行的直线![]() 与椭圆交于不同两点P、Q,
与椭圆交于不同两点P、Q,
若在![]() 轴上存在定点E(
轴上存在定点E(![]() ,0),使
,0),使![]() 恒为定值,求
恒为定值,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)
已知向量![]() 动点
动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() 并且满足
并且满足![]() 其中O是坐标原点,
其中O是坐标原点,![]() 是参数.
是参数.
(I)求动点![]() 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(Ⅱ) 当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(Ⅲ) 如果动点M的轨迹是圆锥曲线,其离心率![]() 满足
满足![]() 求实数
求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)已知向量![]() 动点
动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() 并且满足
并且满足![]() 其中
其中![]() 是坐标原点,
是坐标原点,![]() 是参数.
是参数.
(1)求动点![]() 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(2)当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(3)如果动点![]() 的轨迹是圆锥曲线,其离心率
的轨迹是圆锥曲线,其离心率![]() 满足
满足![]() 求实数
求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com