
下列命题中:(1)若 满足
满足 ,
, 满足
满足 ,则
,则 ;
;
(2)函数 且
且 的图象恒过定点A,若A在
的图象恒过定点A,若A在 上,其中
上,其中 则
则 的最小值是
的最小值是 ; (3)设
; (3)设 是定义在R上,以1为周期的函数,若
是定义在R上,以1为周期的函数,若 在
在 上的值域为
上的值域为 ,则
,则 在区间
在区间 上的值域为
上的值域为 ; (4)已知曲线
; (4)已知曲线 与直线
与直线 仅有2个交点,则
仅有2个交点,则 ; (5)函数
; (5)函数 图象的对称中心为(2,1)。
图象的对称中心为(2,1)。
其中真命题序号为 .
(2)(3)(5)
【解析】
试题分析:
(1) 若 满足
满足 ,则
,则 时,代入左边有
时,代入左边有 ,当
,当 时,代入左边有
时,代入左边有 ,所以此时方程中
,所以此时方程中 ;
; 满足
满足 ,则
,则 时代入左边有
时代入左边有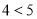 ,当
,当 时代入左边有
时代入左边有 ,所以此时方程中
,所以此时方程中 .
.
所以 ,错误.
,错误.
(2)函数 且
且 的图像恒过定点
的图像恒过定点 ,因为
,因为 在直线
在直线 上,代入有
上,代入有 ,可得
,可得 .则
.则
 ,因为
,因为 所以
所以 ,根据均值不等式可知
,根据均值不等式可知
 ,当且仅当
,当且仅当 ,即
,即 时取得等号.正确.
时取得等号.正确.
(3) 因为函数 在
在 上的值域为
上的值域为 ,设
,设 ,则
,则 ,所以
,所以 ,因为
,因为 是定义在R上,以1为周期的函数,所以
是定义在R上,以1为周期的函数,所以 ,则有
,则有 ,所以此时令
,所以此时令 ,则函数
,则函数 的值域是在
的值域是在 值域基础上上移2个单位得到的为
值域基础上上移2个单位得到的为 ;同理可设
;同理可设 ,通过寻找
,通过寻找 值域关系可得
值域关系可得 的值域为
的值域为 .综上可知
.综上可知 在
在 上的值域为
上的值域为 .正确;
.正确;
(4) 根据曲线方程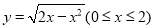 知
知 ,可化简为
,可化简为 ,表示以
,表示以 为圆心,1为半径的圆的
为圆心,1为半径的圆的 轴及其以上部分的曲线.直线
轴及其以上部分的曲线.直线 表示经过定点
表示经过定点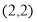 有斜率的直线.因为两者有两个交点,所以画图可知,当直线与曲线相切时,
有斜率的直线.因为两者有两个交点,所以画图可知,当直线与曲线相切时, ,当恰有两个交点时,直线过原点,所以
,当恰有两个交点时,直线过原点,所以 ,综上可知
,综上可知 ,错误.
,错误.
(5) 函数的定义域为 .
.
如果函数 图象的对称中心为
图象的对称中心为 ,那么函数上的点
,那么函数上的点 关于
关于 的对称点
的对称点 也在函数上.
也在函数上.
所以 根据对数的运算法则可得
根据对数的运算法则可得 .即
.即 ;
;
将 代入函数式,
代入函数式, 所以函数过点
所以函数过点 ,显然成立.所以正确.
,显然成立.所以正确.
考点:对数,指数运算;均值不等式,1的代换;周期性应用;直线与曲线的位置关系;中心对称的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1, )处的切线方程
)处的切线方程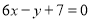 。
。
(1)求函数 的解析式;
的解析式;
(2)求函数 与
与 的图像有三个交点,求
的图像有三个交点,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
设函数
(1)已知 在区间
在区间 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;
(2)存在实数 ,使得当
,使得当 时,
时, 恒成立,求
恒成立,求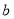 的最大值及此时
的最大值及此时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
①由“若a,b,c∈R,则(ab)c=a(bc)”类比“若a、b、c为三个向量,则(a·b)c=a(b·c)”;
②在数列{an}中,a1=0,an+1=2an+2,猜想an=2n-2;
③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;
上述三个推理中,正确的个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 =
= x+
x+ 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com