练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知的单调递增区间是（ ）

    A. B. C. D.

     

    【解析】

    试题分析：函数是复合函数,其定义域令,即,根据复合函数的单调性:同增异减.该函数是增函数,其外函数是为减函数,其内函数为也必是减函数,所以取区间.

    考点：复合函数单调性的判断.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届山东省高二下学期期中考试文科数学试卷（解析版） 题型：选择题

    设是椭圆上一点，是椭圆的两个焦点， （ ）

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中检测文科数学试卷（解析版） 题型：选择题

    已知中心在原点的椭圆的右焦点为,离心率等于,则椭圆的方程是( )

    A． B．

    C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：填空题

    下列命题中：（1）若满足，满足，则；

    （2）函数且的图象恒过定点Ａ，若Ａ在 上，其中则的最小值是； （3）设是定义在Ｒ上，以１为周期的函数，若在上的值域为，则在区间上的值域为； （4）已知曲线与直线仅有２个交点，则； （5）函数图象的对称中心为（2，1）。

    其中真命题序号为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    下列命题中，真命题是(　　)

    A．?x∈R，ex≤0

    B．?x∈R,2x＞x2

    C．a＋b＝0的充要条件是＝－1

    D．a＞1，b＞1是ab＞1的充分条件

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试文科数学试卷（解析版） 题型：解答题

    某地最近十年粮食需求量逐年上升，下表是部分统计数据：

    年份

    2004

    2006

    2008

    2010

    2012

    需求量(万吨)

    236

    246

    257

    276

    286

     

    (1)利用所给数据求年需求量与年份之间的回归直线方程＝x＋

    (2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试文科数学试卷（解析版） 题型：填空题

    函数

    若在区间上单调递减，则的取值范围　　 　　　．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省济宁市高二5月质量检测理科数学试卷（解析版） 题型：解答题

    已知函数，（）．

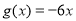    （1）若x＝3是的极值点，求在[1，a]上的最小值和最大值；

    （2）若在时是增函数，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省济宁市高二5月质量检测理科数学试卷（解析版） 题型：解答题

    甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，

    以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：

    （1）打满3局比赛还未停止的概率；

    （2）比赛停止时已打局数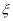的分别列与期望E.

     

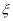    查看答案和解析>>

    同步练习册答案