
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,
以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数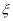 的分别列与期望E
的分别列与期望E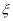 .
.
(1) ;(2)分布列
;(2)分布列
| 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
从而 (局).
(局).
【解析】
试题分析:(1)首先用字母表示事件:如令 分别表示甲、乙、丙在第k局中获胜,由于打满3局比赛还未停止,即在三局比赛中没有人连胜两局,分析其可能情况知为事件
分别表示甲、乙、丙在第k局中获胜,由于打满3局比赛还未停止,即在三局比赛中没有人连胜两局,分析其可能情况知为事件 ,每局比赛的结果相互独立且互斥,利用独立事件、互斥事件的概率求解即可.(2)先写出ξ的所有可能值为2,3,4,5,6,ξ=2的含义是:甲连胜两局或乙连胜两局,故得
,每局比赛的结果相互独立且互斥,利用独立事件、互斥事件的概率求解即可.(2)先写出ξ的所有可能值为2,3,4,5,6,ξ=2的含义是:甲连胜两局或乙连胜两局,故得 ,同理可分别求出ξ取每一个值的概率,列出分布列即可,再利用数学期望公式:
,同理可分别求出ξ取每一个值的概率,列出分布列即可,再利用数学期望公式: 求出
求出 的数学期望.
的数学期望.
试题解析:令 分别表示甲、乙、丙在第k局中获胜.
分别表示甲、乙、丙在第k局中获胜.
(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比赛还未停止的概率为
(2) 的所有可能值为2,3,4,5,6,且
的所有可能值为2,3,4,5,6,且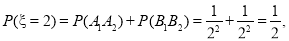




故有分布列
| 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
从而 (局).
(局).
考点:1.互斥、独立事件的概率;2.离散型随机变量的分布列和期望.


科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:填空题
函数 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数.给出下列函数:①
为恒均变函数.给出下列函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
.其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
将函数 的图象向右平移
的图象向右平移 个单位,再将图象上每一点的横坐标缩短到原来的
个单位,再将图象上每一点的横坐标缩短到原来的 倍,所得图象关于直线
倍,所得图象关于直线 对称,则
对称,则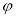 的最小正值为( )
的最小正值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:解答题
命题 :关于
:关于 的不等式
的不等式 对一切
对一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com