
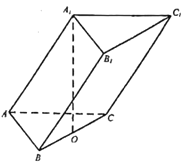
【题目】在三棱柱![]() 中,
中,![]() 是正三角形,
是正三角形,![]() ,点
,点![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰好是
恰好是![]() 中点,侧棱和底面成
中点,侧棱和底面成![]() 角.
角.
(1)求证:![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)二面角![]() 的大小为
的大小为![]() .
.
(3)直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
【解析】
(1)先证明![]() 平面
平面![]() ,根据线面垂直的定义即可得结论;
,根据线面垂直的定义即可得结论;
(2)建立空间直角坐标系,分别求出平面![]() ,平面
,平面![]() 的法向量,求出两法向量的夹角,结合图形即可求解;
的法向量,求出两法向量的夹角,结合图形即可求解;
(3)根据(2)求出的平面![]() 的法向量,结合直线
的法向量,结合直线![]() 的方向向量,即可求解.
的方向向量,即可求解.
(1)连接![]() ,因为
,因为![]() 为
为![]() 的中点,
的中点,![]() 为正三角形,所以
为正三角形,所以![]() ,由点
,由点![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 所以
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系如图.
轴建立空间直角坐标系如图. 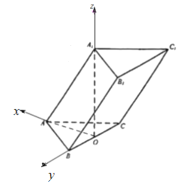 则
则![]() 因为侧棱和底面成
因为侧棱和底面成![]() 角,所以
角,所以![]() ,则
,则![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则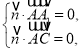 即
即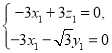 令
令![]() ,则
,则![]() .设平面
.设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则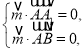 即
即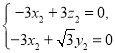 令
令![]() ,则
,则![]() .所以
.所以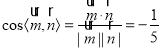 ,由图可知二面角
,由图可知二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的大小为
的大小为![]() .
.
(3)由(2)可知平面![]() 的法向量为
的法向量为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以
,所以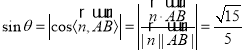 ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角为
所成角为![]()


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】某中学在高二下学期开设四门数学选修课,分别为《数学史选讲》.《球面上的几何》.《对称与群》.《矩阵与变换》.现有甲.乙.丙.丁四位同学从这四门选修课程中选修一门,且这四位同学选修的课程互不相同,下面关于他们选课的一些信息:①甲同学和丙同学均不选《球面上的几何》,也不选《对称与群》:②乙同学不选《对称与群》,也不选《数学史选讲》:③如果甲同学不选《数学史选讲》,那么丁同学就不选《对称与群》.若这些信息都是正确的,则丙同学选修的课程是( )
A. 《数学史选讲》B. 《球面上的几何》C. 《对称与群》D. 《矩阵与变换》
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的纵坐标伸长到原来的
的图象上所有点的纵坐标伸长到原来的![]() 倍(横坐标不变),再向左平移
倍(横坐标不变),再向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,设函数
的图象,设函数![]() .
.
(1)对函数![]() 的解析式;
的解析式;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)若![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() ,
,![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量![]() 与
与![]() ,两组向量
,两组向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均有2个
均有2个![]() 和3个
和3个![]() 按照某种顺序排成一列所构成,记
按照某种顺序排成一列所构成,记![]()
![]() ,且
,且![]() 表示
表示![]() 所有可能取值中的最小值,有以下结论:①有5个不同的值;②若
所有可能取值中的最小值,有以下结论:①有5个不同的值;②若![]() ,则
,则![]() 与
与![]() 无关;③ 若
无关;③ 若![]() ∥
∥![]() ,则
,则![]() 与
与![]() 无关;④ 若
无关;④ 若![]() ,则
,则![]() ;⑤若
;⑤若![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() ;正确的结论的序号是( )
;正确的结论的序号是( )
A.①②④B.②④C.②③D.①⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了测量某塔的高度,某人在一条水平公路![]() 两点进行测量.在
两点进行测量.在![]() 点测得塔底
点测得塔底![]() 在南偏西
在南偏西![]() ,塔顶仰角为
,塔顶仰角为![]() ,此人沿着南偏东
,此人沿着南偏东![]() 方向前进10米到
方向前进10米到![]() 点,测得塔顶的仰角为
点,测得塔顶的仰角为![]() ,则塔的高度为( )
,则塔的高度为( )
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题,
①命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
②命题“若![]() ,则
,则![]() ”的否命题为真命题;
”的否命题为真命题;
③若平面![]() 上不共线的三个点到平面
上不共线的三个点到平面![]() 距离相等,则
距离相等,则![]()
④若![]() ,
,![]() 是两个不重合的平面,直线
是两个不重合的平面,直线![]() ,命题
,命题![]() ,命题
,命题![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
⑤平面![]() 过正方体
过正方体![]() 的三个顶点
的三个顶点![]() ,且
,且![]() 与底面
与底面![]() 的交线为
的交线为![]() ,则
,则![]() ∥
∥![]() ;
;
其中,真命题的序号是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com