
【题目】为了测量某塔的高度,某人在一条水平公路![]() 两点进行测量.在
两点进行测量.在![]() 点测得塔底
点测得塔底![]() 在南偏西
在南偏西![]() ,塔顶仰角为
,塔顶仰角为![]() ,此人沿着南偏东
,此人沿着南偏东![]() 方向前进10米到
方向前进10米到![]() 点,测得塔顶的仰角为
点,测得塔顶的仰角为![]() ,则塔的高度为( )
,则塔的高度为( )
A. 5米B. 10米C. 15米D. 20米
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品![]() 和产品
和产品![]() 需要甲、乙两种新型材料.生产一件产品
需要甲、乙两种新型材料.生产一件产品![]() 需要甲材料
需要甲材料![]() ,乙材料
,乙材料![]() ,并且需要花费1天时间;生产一件产品
,并且需要花费1天时间;生产一件产品![]() 需要甲材料
需要甲材料![]() ,乙材料
,乙材料![]() ,也需要1天时间,生产一件产品
,也需要1天时间,生产一件产品![]() 的利润为1000元,生产一件产品
的利润为1000元,生产一件产品![]() 的利润为2000元.该企业现有甲、乙材料各
的利润为2000元.该企业现有甲、乙材料各![]() ,则在不超过120天的条件下,求生产产品
,则在不超过120天的条件下,求生产产品![]() 、产品
、产品![]() 的利润之和的最大值.
的利润之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面ABCD为梯形,
的底面ABCD为梯形,![]() ,则在面PBC内
,则在面PBC内![]()
![]()

A. 一定存在与CD平行的直线
B. 一定存在与AD平行的直线
C. 一定存在与AD垂直的直线
D. 不存在与CD垂直的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上不重合的四点,
是椭圆上不重合的四点,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,且
,且![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
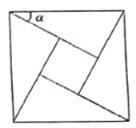
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产![]() 、
、![]() 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于![]() 为正品,小于
为正品,小于![]() 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各![]() 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
|
|
|
|
|
|
B |
|
|
|
|
|
由于表格被污损,数据![]() 、
、![]() 看不清,统计员只记得
看不清,统计员只记得![]() ,且
,且、
![]() 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中![]() 与
与![]() 的值;
的值;
(2)从被检测的![]() 件
件![]() 种元件中任取
种元件中任取![]() 件,求
件,求![]() 件都为正品的概率.
件都为正品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com