
分析 (1)求出切线斜率f′($\frac{1}{2}$),在计算f($\frac{1}{2}$),利用点斜式方程得出切线方程;
(2)求出f(x)的极值点,对极值点与区间[2,4]的关系进行讨论得出f(x)的单调性,从而得出f(x)的最值.
解答 解:(1)a=2时,f(x)=$\frac{x}{ln2x+2}$.f′(x)=$\frac{ln2x+1}{(ln2x+2)^{2}}$.
∴f(x)在($\frac{1}{2}$,f($\frac{1}{2}$))处的切线斜率k=f′($\frac{1}{2}$)=$\frac{1}{4}$.
又f($\frac{1}{2}$)=$\frac{1}{4}$,
∴切线方程为y-$\frac{1}{4}$=$\frac{1}{4}$(x-$\frac{1}{2}$),即2x-8y+1=0.
(2)f′(x)=$\frac{lnax+1}{(lnax+2)^{2}}$,令f′(x)=0得x=$\frac{1}{ae}$.
若a<0,则f(x)在[2,4]上无意义,不符合题意.故a>0.
①若$\frac{1}{ae}$≤2,即a≥$\frac{1}{2e}$时,当x∈[2,4]时,f′(x)>0,∴f(x)在[2,4]上是增函数,
∴fmin(x)=f(2)=$\frac{2}{ln2a+2}$,fmax(x)=f(4)=$\frac{4}{ln4a+2}$.
②若$\frac{1}{ae}$≥4,即a≤$\frac{1}{4e}$时,当x∈[2,4]时,f′(x)<0,∴f(x)在[2,4]上是减函数,
∴fmin(x)=f(4)=$\frac{4}{ln4a+2}$,fmax(x)=f(2)=$\frac{2}{ln2a+2}$.
③若2<$\frac{1}{ae}$<4,即$\frac{1}{4e}<a<\frac{1}{2e}$,则f(x)在[2,$\frac{1}{ae}$)上单调递减,在($\frac{1}{ae}$,4]上单调递增.
∴fmin(x)=f($\frac{1}{ae}$)=$\frac{1}{ae}$,fmax(x)=f(2)=$\frac{2}{ln2a+2}$.
点评 本题考查了导数的几何意义,导数与函数单调性的关系,函数最值的计算,分类讨论思想,属于中档题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
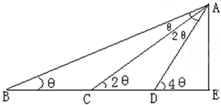 在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com