
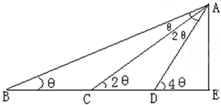
 在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高. 分析 由题意及仰角的定义,利用数形结合的思想,利用图形中角与角的联系,求出θ=15°,即可得出结论.
解答 解:由已知BC=30米,CD=10$\sqrt{3}$米,∠ABE=θ,∠ACE=2θ,∠ADE=4θ,
在Rt△ABE中,BE=AEcotθ,
在Rt△ACE中,CE=AEcot2θ,
∴BC=BE-CE=AE(cotθ-cot2θ).
同理可得:CD=AE(cot2θ-cot4θ).
∴$\frac{BC}{DC}$=$\frac{AE(cotθ-cot2θ)}{AE(cot2θ-cot4θ)}$,
即$\frac{cotθ-cot2θ}{cot2θ-cot4θ}$=$\sqrt{3}$,
而cotθ-cot2θ=$\frac{sin2θcosθ-cos2θsinθ}{sinθsin2θ}$=$\frac{1}{sin2θ}$.
同理可得cot2θ-cot4θ=$\frac{1}{sin4θ}$.
∴$\frac{sin4θ}{sin2θ}$=2cos2θ=$\sqrt{3}$
∴cos2θ=$\frac{\sqrt{3}}{2}$,结合题意可知:2θ=30°,θ=15°,
∴AE=$\frac{BC}{cotθ-cot2θ}$=BCsin2θ=15m.
点评 本题考查了学生会从题意中抽取出图形进而分析问题,考查了学生们利用三角形解出三角形的边与角,及二倍角的正切公式,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
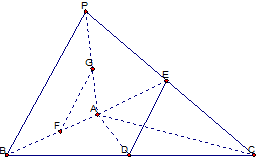 如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F,G分别为BC,PC,AB,PA的中点.
如图,在四面体P-ABC中,PA⊥平面ABC,AB=3,AC=4,BC=5,且D,E,F,G分别为BC,PC,AB,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 3 | 7 | 10 |
| 总计 | 25 | 15 | 40 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
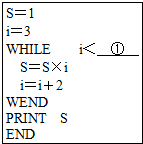 设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线 ①上不能填入的数是( )
设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线 ①上不能填入的数是( )| A. | 13 | B. | 13.5 | C. | 14 | D. | 14.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com