
分析 (1)求出函数的导函数即得极大值;
(2)通过分析,问题转化求g(x)=$\frac{xlnx+x}{x-1}$,在x∈(1,+∞)上的最小值点,计算即可.
(3)通过分析得函数p(x)=$\frac{lnx}{x}$+1与y=m在区间[1,e2]上有且仅有一个交点,利用p(x)的单调性,比较p(1)、p(e2)的大小即可;
解答 解:(1)∵f′(x)=1+lnx,x>0,
令f′(x)=1+lnx=0,解得x=$\frac{1}{e}$,
∵当x∈(0,$\frac{1}{e}$)时,f′(x)<0,函数单调递减,
当x∈($\frac{1}{e}$,+∞)时,f′(x)>0,函数单调递增,
∴f(x)min=f($\frac{1}{e}$)=$\frac{1}{e}$ln$\frac{1}{e}$=-$\frac{1}{e}$,无最大值,
(2)令g(x)=$\frac{f(x)+x}{x-1}$=$\frac{xlnx+x}{x-1}$,x>1
则g′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$,
令h(x)=x-lnx-2(x>1),则h′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0,
∴函数h(x)在(1,+∞)上单调递增.
∵h(3)=1-ln3<0,h(4)=2-2ln2>0,
∴方程h(x)=0在(1,+∞)上存在唯一实根x0,且满足x0∈(3,4).
当1<x<x0时,h(x)<0,即g′(x)<0,
当x>x0时,h(x)>0,即g′(x)>0,
∴函数g(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增.
∴g(x)min=g(x0)=$\frac{{x}_{0}(1+ln{x}_{0})}{{x}_{0}-1}$=$\frac{{x}_{0}(1+{x}_{0}-2)}{{x}_{0}-1}$=x0∈(3,4).
∴k<g(x)min=x0,
∵x0∈(3,4),
∴整数k的最大值是3.
(3)方程f(x)+x2=mx2在区间[1,e2]内唯一实数解,
即xlnx+x2=mx2在区间[1,e2]内唯一实数解,
化简得$\frac{lnx}{x}$+1=m在区间[1,e2]内唯一实数解,
记p(x)=$\frac{lnx}{x}$+1,则p′(x)=$\frac{1-lnx}{{x}^{2}}$,
则当x∈[1,e)时,p′(x)>0,
当x∈(e,e2]时,p′(x)<0,
∵p(1)=1,p(e2)=1+$\frac{2}{{e}^{2}}$,
∴m∈[1,1+$\frac{2}{{e}^{2}}$].
点评 本题考查了利用导数研究曲线的最值,参数的取值范围考查了数学转化思想,关键是构造函数,学生思考起来有一定难度,此题属于难度较大的题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
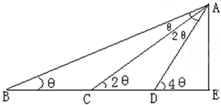 在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
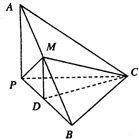 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com