
分析 logb(3a-1)为正数,即有b>1,且3a-1>1,即a>$\frac{2}{3}$;或0<b<1且0<3a-1<1,即$\frac{1}{3}$<a<$\frac{2}{3}$.圆(x-$\frac{1}{2}$)2+(y+$\frac{1}{3}$)2=c2上的圆心为P($\frac{1}{2}$,-$\frac{1}{3}$),半径为c,以(b,a)为直角坐标,作出不等式表示的平面区域,通过圆的半径的变化,即可得到所求范围.
解答 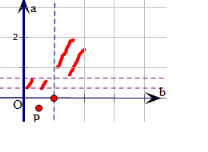 解:logb(3a-1)为正数,即有
解:logb(3a-1)为正数,即有
b>1,且3a-1>1,即a>$\frac{2}{3}$;
或0<b<1且0<3a-1<1,即$\frac{1}{3}$<a<$\frac{2}{3}$.
圆(x-$\frac{1}{2}$)2+(y+$\frac{1}{3}$)2=c2上的圆心为P($\frac{1}{2}$,-$\frac{1}{3}$),半径为c,
以(b,a)为直角坐标,不等式$\left\{\begin{array}{l}{b>1}\\{a>\frac{2}{3}}\end{array}\right.$和$\left\{\begin{array}{l}{0<b<1}\\{\frac{1}{3}<a<\frac{2}{3}}\end{array}\right.$表示的区域如图中斜线部分(不含边界),
则以P为圆心,画圆,观察可得$\frac{2}{3}$<c<$\sqrt{(1-\frac{1}{2})^{2}+(\frac{2}{3}+\frac{1}{3})^{2}}$即为$\frac{2}{3}$<c<$\frac{\sqrt{5}}{2}$;或c>$\frac{\sqrt{5}}{2}$.
故答案为:($\frac{2}{3}$,$\frac{\sqrt{5}}{2}$)∪($\frac{\sqrt{5}}{2}$,+∞).
点评 本题考查对数函数的定义域,同时考查不等式表示的平面区域的运用,考查数形结合的思想方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 99 | B. | 100 | C. | 101 | D. | 102 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
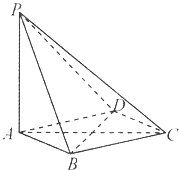 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com