
分析 (1)根据数列的递推关系求出数列的通项公式,结合等比数列的通项公式即可求a2+a4+a6+…+a2n+2的和;
(2)求出数列{cn}的通项公式,利用错位相减法进行求解即可.
解答 解:(1)∵Sn=2n+1-2,
∴当n≥2时,an=Sn-Sn-1=2n+1-2-2n+2=2n+1-2n=2n,
当n=1时,a1=22-2=4-2=2,满足an=2n,
∴数列{an}的通项公式an=2n,
则a2n=22n=4n,
则数列{a2n}是公比q=4的等比数列,
则a2+a4+a6+…+a2n+2=$\frac{4(1-{4}^{n+1})}{1-4}$=$\frac{4}{3}$(4n+1-1);
(2)∵bn2-(n-1)bn-2(n+1)=0,
∴(bn+2)[bn-(n+1)]=0,
∵正项数列{bn}中,bn>0,
∴bn-(n+1)=0,
即bn=n+1,
则cn=$\frac{{b}_{n}}{{a}_{n}}$=$\frac{n+1}{{2}^{n}}$,
则Tn=$\frac{2}{{2}^{1}}$+$\frac{3}{{2}^{2}}$+$\frac{4}{{2}^{3}}$+…+$\frac{n}{{2}^{n-1}}$+$\frac{n+1}{{2}^{n}}$,
则$\frac{1}{2}$Tn=$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{4}{{2}^{4}}$+…+$\frac{n}{{2}^{n}}$+$\frac{n+1}{{2}^{n+1}}$,
两式作差得$\frac{1}{2}$Tn=$\frac{2}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{n+1}{{2}^{n}}$=$\frac{2}{{2}^{1}}$+$\frac{\frac{1}{{2}^{2}}(1-\frac{1}{{2}^{n-2}})}{1-\frac{1}{2}}$-$\frac{n+1}{{2}^{n}}$=1+$\frac{1}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{n+1}{{2}^{n}}$
=$\frac{3}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{n+1}{{2}^{n}}$.
点评 本题主要考查递推数列的应用,以及数列求和,求出数列的通项公式,利用公式法或错位相减法是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
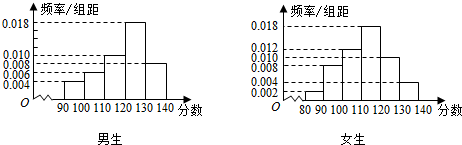
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com