
分析 (1)利用作差法,即可证明结论;
(2)利用正弦定理,证明$\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}<2$即可利用(1)的结论,即可证明.
解答 证明:(1)∵m>n>0,p>0,$左-右=\frac{(n-m)p}{m(m+p)}<0$,
∴$\frac{n}{m}<\frac{n+p}{m+p}$;
(2)利用正弦定理,证明$\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}<2$即可.
由(1)得:$\frac{c}{a+b}$<$\frac{2c}{a+b+c}$,$\frac{a}{b+c}$<$\frac{2a}{a+b+c}$,$\frac{b}{c+a}$<$\frac{2b}{c+a+b}$,
三式相加可得$\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}<2$,
∴$\frac{sinC}{sinA+sinB}+\frac{sinA}{sinB+sinC}+\frac{sinB}{sinC+sinA}<2$.
点评 本题考查不等式的证明,考查作差法的运用,考查学生分析解决问题的能力,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处就没有切线 | |
| B. | 若曲线y=f(x)在点(x0,y0)处有切线,则f′(x0)必存在 | |
| C. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处的切线斜率不存在 | |
| D. | 若曲线y=f(x)在点(x0,y0)处没有切线,则f′(x0)有可能存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
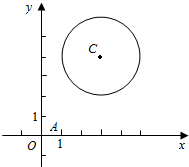 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com