
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若函数![]() 对任意
对任意![]() ,有
,有![]() ,求函数
,求函数![]() 在[﹣
在[﹣![]() ,
,![]() ]上的值域.
]上的值域.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)逆用正弦的和角公式及降幂公式,可化得f(x)= ![]() sin2x+
sin2x+![]() ,由公式
,由公式![]() 可求得周期。(2)由题意可得g(x)
可求得周期。(2)由题意可得g(x)![]() , 由
, 由![]() [﹣
[﹣![]() ,
,![]() ],求得整体角范围2x+
],求得整体角范围2x+![]() ∈
∈![]() ,则
,则![]() ≤sin(2x+
≤sin(2x+![]() )≤1,可求得值域。
)≤1,可求得值域。
试题解析:(1)f(x)=![]() sin(2x+
sin(2x+![]() )+sin2x
)+sin2x
=![]()
=![]() sin2x+
sin2x+![]() cos2x+sin2x
cos2x+sin2x
=![]() sin2x+
sin2x+![]()
=![]() sin2x+1﹣
sin2x+1﹣![]() =
=![]() sin2x+
sin2x+![]() ,
,
∴f(x)的最小正周期T=![]() ;
;
(2)∵函数g(x)对任意x∈R,有g(x)=f(x+![]() ),
),
∴g(x)=![]() sin2(x+
sin2(x+![]() )+
)+![]() =
=![]() sin(2x+
sin(2x+![]() )+
)+![]() ,
,
当x∈[﹣![]() ,
,![]() ]时,则2x+
]时,则2x+![]() ∈
∈![]() ,
,
则![]() ≤sin(2x+
≤sin(2x+![]() )≤1,即
)≤1,即![]() ×
×![]() ≤g(x)
≤g(x)![]() ,解得
,解得![]() ≤g(x)≤1.
≤g(x)≤1.
综上所述,函数g(x)在[﹣![]() ,
,![]() ]上的值域为:[
]上的值域为:[![]() ,1].
,1].


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
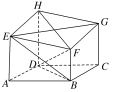
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=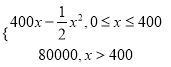 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2-4|x|-5.
(Ⅰ)画出y=f(x)的图象;
(Ⅱ)设A={x|f(x)≥7},求集合A;
(Ⅲ)方程f(x)=k+1有两解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com