
【题目】如图,已知四边形![]() 和
和![]() 均为直角梯形,
均为直角梯形,![]() ,
,![]() 且
且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
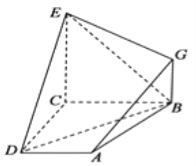
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
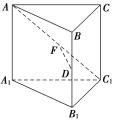
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是![]() ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是![]() .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记![]() 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ;
;
(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com