练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需要增加投入100元，已知总收益满足函数：R(x)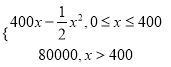＝其中x是仪器的月产量．当月产量为何值时，公司所获得利润最大？最大利润是多少？

    【答案】当月产量为300台时，公司所获利润最大，最大利润是25 000元．

    【解析】试题分析：一般要根据题意写出利润关于产量的函数，注意不同条件对应利润不同，所以要写成分段函数，然后利用二次函数性质求最值，分段函数最值注意比较两段的最值得大小.

    试题解析：（1）设月产量为x台,则总成本为20000+ 100x,从而利润

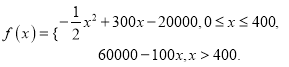
    当0≦x≦400时，f(x)= 所以当x=300时，有最大值25000；

    当x>400时，f(x)=60000-100x是减函数，

    所以f(x)= 60000-100×400<25000。

    所以当x=300时，有最大值25000，

    即当月产量为300台时，公司所获利润最大，最大利润是25000元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点，圆．

    （1）若过点的圆的切线只有一条，求的值及切线方程；

    （2）若过点且在两坐标轴上截距相等的直线与圆相切，求的值及切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某市的高一学生中随机抽取400名同学的体重进行统计，得到如图所示频率分布直方图.

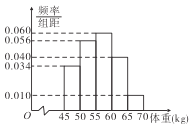
    （Ⅰ）估计从该市高一学生中随机抽取一人，体重超过的概率；

    （Ⅱ）假设该市高一学生的体重服从正态分布.

    （ⅰ）利用（Ⅰ）的结论估计该高一某个学生体重介于 之间的概率；

    （ⅱ）从该市高一学生中随机抽取3人，记体重介于之间的人数为，利用（ⅰ）的结论，求的分布列及.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图几何体是四棱锥，为正三角形，，且．

    （1）求证: 平面平面；

    （2）是棱的中点，求证:平面；

    （3）求四棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在坐标原点，长轴在轴上，分别在其左、右焦点，在椭圆上任意一点，且的最大值为1，最小值为．

    （1）求椭圆的方程；

    （2）设为椭圆的右顶点，直线是与椭圆交于两点的任意一条直线，若，证明直线过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，若

    （1）求函数的解析式；

    （2）画出函数的图象，并说出函数的单调区间；

    （3）若，求相应的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数的最小正周期；

    （2）若函数对任意，有，求函数在[﹣ ，]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题实数满足 ；命题实数满足.

    （1）当时，若“且”为真，求实数的取值范围；

    （2）若“非”是“非”的必要不充分条件，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，

    初赛采用选手选一题答一题的方式进行，每位选手最多有次选题答题的机会，选手累计答对题或答错题即终止其初赛的比赛，答对题者直接进入决赛，答错题者则被淘汰．已知选手甲答题的正确率为．

    (1) 求选手甲可进入决赛的概率；

    (2) 设选手甲在初赛中答题的个数为，试写出的分布列，并求的数学期望．

    查看答案和解析>>

    同步练习册答案