Question

7．如图，在三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，AB=2，AC=PA=4．
（1）求直线PB与平面PAC所成角的正弦值；
（2）求二面角A-PC-B的余弦值．

Answer 1

分析 以A为原点，在平面ABC内作垂直于AC的射线为x轴，以射线AC为y轴，
射线AP为z轴建立如图所示空间直角坐标系，则P（0，0，4），B（$\sqrt{3}$，1，0），C（0，4，0），利用向量法求解

解答 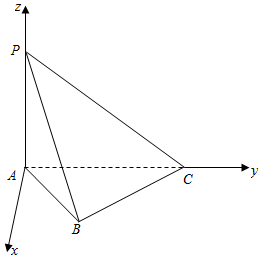解：（1）如图，以A为原点，在平面ABC内作垂直于AC的射线为x轴，以射线AC为y轴，
射线AP为z轴建立如图所示空间直角坐标系，…（2分）
则P（0，0，4），B（$\sqrt{3}$，1，0），C（0，4，0），故$\overrightarrow{PB}=（\sqrt{3}，1，-4）$，
由x轴⊥平面PAC得平面PAC的一个法向量为$\overrightarrow{n}=（1，0，0）$，…（5分）
设直线PB与平面PAC所成角为α，
则sinα=|cos$＜\overrightarrow{n}，\overrightarrow{PB}＞$|=|$\frac{\overrightarrow{PB}•\overrightarrow{n}}{|\overrightarrow{n}||\overrightarrow{PB}|}$|=$\frac{\sqrt{3}}{\sqrt{20}}$=$\frac{\sqrt{15}}{10}$，
即直线PB与平面PAC所成角的正弦值为$\frac{\sqrt{15}}{10}$．…（8分）
（2）∵$\overrightarrow{PC}=（0，4，-4）$，$\overrightarrow{BC}=（-\sqrt{3}，3，0）$，
设$\overrightarrow{m}$=（x，y，z）为平面PBC的一个法向量，
则$\overrightarrow{m}•\overrightarrow{PC}=4y-4z=0$，$\overrightarrow{m}•\overrightarrow{BC}=-\sqrt{3}x+3y=0$，
可取$\overrightarrow{m}=（\sqrt{3}，1，1）$为平面PBC的一个法向量，…（11分）
可知平面PAC的一个法向量为$\overrightarrow{n}=（1，0，0）$，
设二面角A-PC-B的平面角为β，则β为锐角，则cosβ=|cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞|=$\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5}$，
即二面角A-PC-B的余弦值为$\frac{\sqrt{15}}{5}$．…（14分）

点评 本题考查了利用向量法求线面角、二面角，属于中档题．