
【题目】给出下列命题:①已知 ![]() ,“
,“ ![]() 且
且 ![]() ”是“
”是“ ![]() ”的充分条件;
”的充分条件;
②已知平面向量 ![]() ,
, ![]() 是“
是“ ![]() ”的必要不充分条件;
”的必要不充分条件;
③已知 ![]() ,“
,“ ![]() ”是“
”是“ ![]() ”的充分不必要条件;
”的充分不必要条件;
④命题 ![]() “
“ ![]() ,使
,使 ![]() 且
且 ![]() ”的否定为
”的否定为 ![]() “
“ ![]() ,都有
,都有 ![]() 且
且 ![]() ”.其中正确命题的个数是( )
”.其中正确命题的个数是( )
A.0
B.1
C.2
D.3
【答案】C
【解析】①已知 ![]() ,“
,“ ![]() 且
且 ![]() ”能够推出“
”能够推出“ ![]() ”,“
”,“ ![]() ”不能推出“
”不能推出“ ![]() ”,本选项正确;
”,本选项正确;
②已知平面向量 ![]() , “
, “ ![]() ”不能推出“
”不能推出“ ![]() ”,本选项不正确;
”,本选项不正确;
③已知 ![]() ,“
,“ ![]() ”是“
”是“ ![]() ”的充分不必要条件,正确;
”的充分不必要条件,正确;
④命题 ![]() “
“ ![]() ,使
,使 ![]() 且
且 ![]() ”的否定为
”的否定为 ![]() “
“ ![]() ,都有
,都有 ![]() 或
或 ![]() ”本选项不正确.
”本选项不正确.
正确的个数为2.
故答案为:C
(1)当a > 1 且 b > 1 时,可以推出 a b > 1,但是 a b > 1不能推出 a > 1 且 b > 1,可判断是正确的;
(2)结合平面向量的几何性质可知模都大于1,并不能推出向量的和的模大于1,故不正确;
(3)a,b的平方和不小于1,则a,b的绝对值的和也不小于1,正确;
(4)且命题的否定一定是用或连接,特称命题的否定是全称命题.


科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的参数方程为
的参数方程为  (
( ![]() 为参数).
为参数).
(Ⅰ)求曲线 ![]() 和直线
和直线 ![]() 的普通方程;
的普通方程;
(Ⅱ)若点 ![]() 为曲线
为曲线 ![]() 上一点,求点
上一点,求点 ![]() 到直线
到直线 ![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次 ![]() 知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.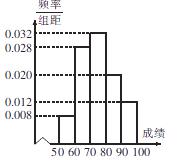
(1)试确定受奖励的分数线;
(2)从受奖励的20人中利用分层抽样抽取5人,再从抽取的5人中抽取2人在主会场服务,试求2人成绩都在90分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为 ![]() .
.
(I)求椭圆C的方程;
(II)设过点B(0,m)(m>0)的直线 ![]() 与椭圆C相交于E,F两点,点B关于原点的对称点为D,若点D总在以线段EF为直径的圆内,求m的取值范围.
与椭圆C相交于E,F两点,点B关于原点的对称点为D,若点D总在以线段EF为直径的圆内,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示:

(1)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(2)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中哪个学校地理成绩较好?(不要求计算,要求写出理由);
(3)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com