Question

11．将函数f（x）=2cos（2x-$\frac{π}{6}}$）的图象向左平移$\frac{π}{4}$个单位得到g（x）的图象，记函数g（x）在区间$[{t，t+\frac{π}{4}}]$内的最大值为M_t，最小值为m_t，记h_t=M_t-m_t，若t∈[${\frac{π}{4}$，$\frac{π}{2}}$]，则函数h（t）的最小值为1．

Answer 1

分析 求出g（x）的解析式，判断g（x）的单调性，根据g（x）的图象得出h（t）取得最小值时对应的t的值，从而计算出M_t，m_t，得出答案．

解答 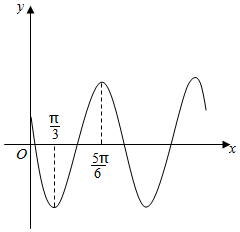解：g（x）=2cos[2（x+$\frac{π}{4}$）-$\frac{π}{6}$]=2cos（2x+$\frac{π}{3}$），
∴g（x）在（$\frac{π}{4}$，$\frac{π}{3}$）上单调递减，在（$\frac{π}{3}$，$\frac{3π}{4}$）上单调递增，
∴当$\frac{π}{4}$≤t≤$\frac{π}{3}$时，g（x）在区间$[{t，t+\frac{π}{4}}]$内先减后增，
当$\frac{π}{3}$$＜t≤\frac{π}{2}$时，g（x）在区间$[{t，t+\frac{π}{4}}]$内单调递增，
∴当t=$\frac{π}{4}$时，h（t）取得最小值，此时M_t=g（$\frac{π}{2}$）=-1，m_t=g（$\frac{π}{3}$）=-2，
∴函数h（t）的最小值为-1-（-2）=1．
故答案为1．

点评 本题考查了三角函数的图象与性质，属于中档题．