
【题目】新型冠状病毒肺炎正在全球蔓延,对世界经济影响严重,中国疫情防控,复工复学恢复经济成为各国的榜样,绵阳某商场在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有2种服装商品的概率;
(2)商场对选的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高300元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金,假设顾客每次抽奖时获奖与否是等概率的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
【答案】(1)![]() ;(2)商场应将中奖奖金数额最高定为200元.
;(2)商场应将中奖奖金数额最高定为200元.
【解析】
(1)选出3种商品进行促销活动,至少有2种服装商品的情况有两种,分类讨论即可确定其概率.
(2)根据题意可知中奖次数符合二项分布,因而可求得中将次数的期望,即可求得最高的定价.
(1)从3种服装商品、2种家电、4种日用商品中,选出3种商品进行促销活动,至少有2种服装商品的情况有两种:
有2种服装商品:![]() ;
;
有3种服装商品:![]() ;
;
所以至少有2种服装商品的概率为![]() .
.
(2)顾客每次抽奖时获奖与否是等概率,则中奖概率为![]() ,
,
因为有3次抽奖的机会,符合二项分布,因而![]() ,
,
则中将次数的数学期望为![]() ,
,
设每次奖金金额为![]() ,则
,则![]() ,
,
解得![]()
所以商场应将中奖奖金数额最高定为200元.


科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
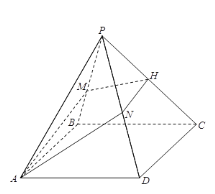
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图放置的边长为2的正方形ABCD沿
中,如图放置的边长为2的正方形ABCD沿![]() 轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点
轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
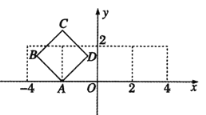
A.函数![]() 在
在![]() 上有两个零点
上有两个零点
B.函数![]() 是偶函数
是偶函数
C.函数![]() 在
在![]() 上单调递增
上单调递增
D.对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 为解释变量,
为解释变量,![]() 为预报变量,若以
为预报变量,若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() ;若以
;若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() .
.
(1)判断![]() 与
与![]() 哪一个更适宜作为国内生产总值(GDP)近似值
哪一个更适宜作为国内生产总值(GDP)近似值![]() 关于年份代号
关于年份代号![]() 的回归方程,并说明理由;
的回归方程,并说明理由;
(2)根据(1)的判断结果及表中数据,求出![]() 关于年份代号
关于年份代号![]() 的回归方程(系数精确到
的回归方程(系数精确到![]() );
);
(3)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
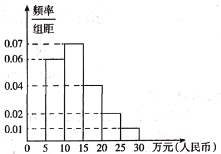
以(2)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: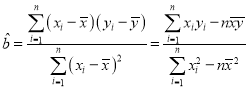 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com