
【题目】已知数列![]() 满足
满足![]() ,
,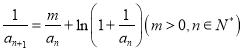 .求证:当
.求证:当![]() 时,
时,
(Ⅰ)![]() ;
;
(Ⅱ)当![]() 时,有
时,有![]() ;
;
(Ⅲ)当![]() 时,有
时,有![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)见解析
【解析】
(Ⅰ)通过数学归纳法,即可证明![]() ;
;
(Ⅱ)先通过构造函数![]() ,利用其单调性
,利用其单调性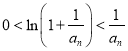 ,对递推公式放缩,得到
,对递推公式放缩,得到![]() ,再利用累乘法即可证明
,再利用累乘法即可证明![]() ;
;
(Ⅲ)通过构造函数![]() ,由导数证明
,由导数证明![]() 在
在![]() 上恒成立,从而得
上恒成立,从而得![]() ,再根据放缩法可得
,再根据放缩法可得![]() ,变形得到
,变形得到![]() ,由累乘法即可证出.
,由累乘法即可证出.
(Ⅰ)用数学归纳法进行证明.
①当![]() 时,
时,![]() 成立;
成立;
②假设当![]() 时,有
时,有![]() 成立,则当
成立,则当![]() 时,有
时,有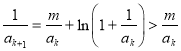 ,又
,又![]() ,故
,故![]() ,综上,可知当
,综上,可知当![]() 时,均有
时,均有![]() .
.
(Ⅱ)设![]() ,则
,则![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
因为 ,即
,即![]() ,
,
当![]() 时,由累乘法可得,
时,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ;
;
因为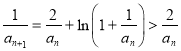 ,即
,即![]() ,
,
当![]() 时,由累乘法可得,
时,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ,
,
故当![]() 时,有
时,有![]() ;
;
(Ⅲ)由(Ⅱ)可知, 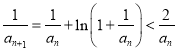 ,即
,即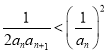 ,且
,且![]() .
.
设![]() ,
,![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以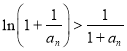 ,
,
因为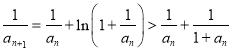 ,
,
即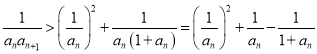 ,且
,且![]() ,
,
所以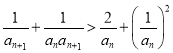 ,即
,即 ,
,
故有![]() ,变形为
,变形为![]() ,
,
当![]() 时,所以
时,所以![]() ,
,
又![]() ,即
,即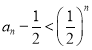 ,所以
,所以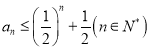 .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
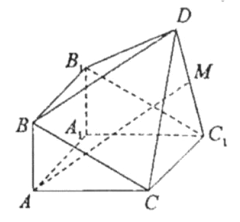
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 、
、![]() 两点分别是椭圆
两点分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,直线
的动点,直线![]() 、
、![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 、
、![]() 两点,点
两点,点![]() ,试问:
,试问:![]() 外接圆是否恒过
外接圆是否恒过![]() 轴上的定点(异于点
轴上的定点(异于点![]() )?若是,求该定点坐标;若否,说明理由.
)?若是,求该定点坐标;若否,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎正在全球蔓延,对世界经济影响严重,中国疫情防控,复工复学恢复经济成为各国的榜样,绵阳某商场在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有2种服装商品的概率;
(2)商场对选的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高300元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金,假设顾客每次抽奖时获奖与否是等概率的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在脱贫攻坚中,某市教育局定点帮扶前进村![]() 户贫困户.驻村工作队对这
户贫困户.驻村工作队对这![]() 户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限
户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限![]() 年”与“家庭平均受教育年限
年”与“家庭平均受教育年限![]() 年”,具体调査结果如下表所示:
年”,具体调査结果如下表所示:
平均受教育年限 | 平均受教育年限 | 总计 | |
绝对贫困户 | 10 | 40 | 50 |
相对贫困户 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
(1)为了参加扶贫办公室举办的贫困户“谈心谈话”活动,现通过分层抽样从“家庭平均受教育年限![]() 年”的
年”的![]() 户贫困户中任意抽取
户贫困户中任意抽取![]() 户,再从所抽取的
户,再从所抽取的![]() 户中随机抽取
户中随机抽取![]() 户参加“谈心谈话”活动,求至少有
户参加“谈心谈话”活动,求至少有![]() 户是绝对贫困户的概率;
户是绝对贫困户的概率;
(2)根据上述表格判断:是否有![]() 的把握认为贫困程度与家庭平均受教育程度有关?
的把握认为贫困程度与家庭平均受教育程度有关?
参考公式:![]()
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
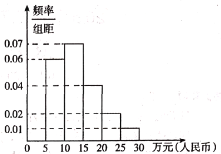
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: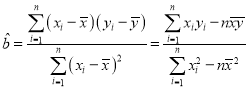 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数![]() 是奇函数”.
是奇函数”.
(Ⅰ)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅱ)求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅲ)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的充要条件为“存在实数
的图象关于某直线成轴对称图象”的充要条件为“存在实数![]() 和
和![]() ,使得函数
,使得函数![]() 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com