
分析 (1)由an=$\frac{3n{a}_{n-1}}{2{a}_{n-1}+n-1}$(n≥2,n∈N).两边取倒数:即可化为$\frac{n}{{a}_{n}}-1$=$\frac{1}{3}(\frac{n-1}{{a}_{n-1}}-1)$,利用等比数列的通项公式即可得出;
(2)欲证原结论,只需证$\frac{1}{2}$<$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{n}})$,先用数学归纳法证:$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{n}})$≥$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{n}}$,即可得出.
解答 证明:(1)由an=$\frac{3n{a}_{n-1}}{2{a}_{n-1}+n-1}$(n≥2,n∈N).两边取倒数:$\frac{1}{{a}_{n}}$=$\frac{2}{3n}+\frac{n-1}{3n{a}_{n-1}}$,化为$\frac{n}{{a}_{n}}-1$=$\frac{1}{3}(\frac{n-1}{{a}_{n-1}}-1)$,
∴数列$\{\frac{n}{{a}_{n}}-1\}$是首项$\frac{1}{{a}_{1}}$-1=-$\frac{1}{3}$,公比q=$\frac{1}{3}$等比数列,
∴$\frac{n}{{a}_{n}}$-1=$-(\frac{1}{3})^{n}$,
∴an=$\frac{n•{3}^{n}}{{3}^{n}-1}$.
(2)欲证原结论,只需证$\frac{1}{2}$<$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{n}})$,
现先用数学归纳法证:$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{n}})$≥$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{n}}$,(*)
当n=1时,左右两边显然相等.
假设n=k时,$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{k}})$≥$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$,
则n=k+1时,$(1-\frac{1}{3})(1-\frac{1}{{3}^{2}})(1-\frac{1}{{3}^{3}})$•…•$(1-\frac{1}{{3}^{k}})$$•(1-\frac{1}{{3}^{k+1}})$≥($1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$)$(1-\frac{1}{{3}^{k+1}})$,
∵($1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$)$(1-\frac{1}{{3}^{k+1}})$=$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$+$\frac{1}{{3}^{k+1}}$•$(\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{k}})$
=$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$+$\frac{1}{{3}^{k+1}}$$•\frac{\frac{1}{3}(1-\frac{1}{{3}^{k}})}{1-\frac{1}{3}}$≥$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{k}}$-$\frac{1}{{3}^{k+1}}$.
由数学归纳法可知:(*)对于?n∈N*都成立.
又$1-\frac{1}{3}-\frac{1}{{3}^{2}}$-…-$\frac{1}{{3}^{n}}$=1-$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=1-$\frac{1}{2}(1-\frac{1}{{3}^{n}})$>$\frac{1}{2}$,
故原命题成立.
点评 本题考查了“取倒数法”、等比数列的通项公式、“数学归纳法”、不等式的性质、“放缩法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
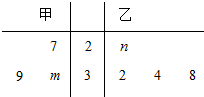 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BD}$=$\frac{7}{13}$$\overrightarrow{BC}$ | B. | $\overrightarrow{BD}$=$\frac{6}{13}$$\overrightarrow{BC}$ | C. | $\overrightarrow{BD}$=$\frac{13}{7}$$\overrightarrow{BC}$ | D. | $\overrightarrow{BD}$=$\frac{13}{6}$$\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
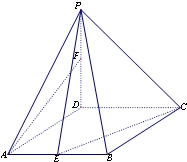 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com