
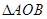 是抛物线
是抛物线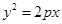 (p>0)的内接正三角形(
(p>0)的内接正三角形(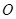 为坐标原点),其面积为
为坐标原点),其面积为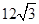 ;点M是直线
;点M是直线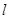 :
: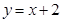 上的动点,过点M作抛物线的切线MP、MQ,P、Q为切点.
上的动点,过点M作抛物线的切线MP、MQ,P、Q为切点. MPQ面积的最小值及相应的直线PQ的方程.
MPQ面积的最小值及相应的直线PQ的方程.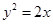 ; (2)直线PQ过定点
; (2)直线PQ过定点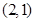 ;
;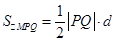
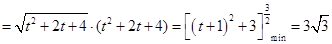
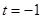 ,
, MPQ面积有最小值
MPQ面积有最小值 .此时直线PQ的方程是:
.此时直线PQ的方程是: ..
..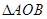 面积是
面积是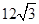 ,设边长为
,设边长为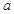 ,
, ................................1'
................................1' ,
,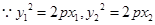 ,
,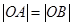
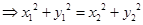 ,
,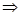

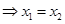 ,所以点A,B关于
,所以点A,B关于 轴对称,..............2'
轴对称,..............2'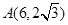 可得
可得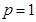 ,抛物线方程是:
,抛物线方程是: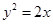 ;....................4'
;....................4' ,切点
,切点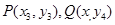 ,则切线MP:
,则切线MP: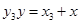 ,MQ:
,MQ: ,相较于M,所以
,相较于M,所以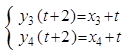 ,可得直线PQ的方程:
,可得直线PQ的方程:
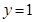 时,
时,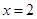 与
与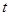 无关,所以直线PQ过定点
无关,所以直线PQ过定点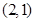 ;.....................8'
;.....................8' ,
,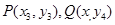 ,由(2)知直线PQ的方程是:
,由(2)知直线PQ的方程是: ,
,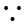
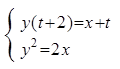

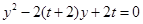 ,
,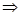

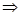
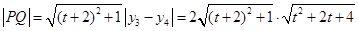 ,.............10'
,.............10'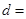
 ,
,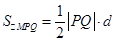
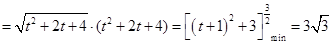 ....12'
....12'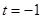 ,
, MPQ面积有最小值
MPQ面积有最小值 .此时直线PQ的方程是:
.此时直线PQ的方程是: ..
..

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源:不详 题型:解答题
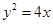 的焦点为
的焦点为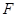 ,过点
,过点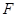 的直线交抛物线于
的直线交抛物线于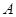 ,
,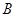 两点.
两点.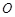 为坐标原点,求证:
为坐标原点,求证: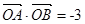 ;
;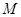 在线段
在线段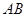 上运动,原点
上运动,原点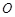 关于点
关于点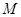 的对称点为
的对称点为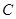 ,求四边形
,求四边形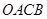 面积的最小值..
面积的最小值..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
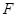 是抛物线
是抛物线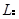
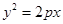
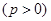 的焦点,
的焦点,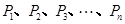 是抛物线
是抛物线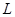 上的
上的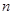 个不同的点(
个不同的点(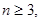
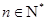 ).
).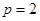 时,试写出抛物线
时,试写出抛物线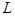 上的三个定点
上的三个定点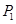 、
、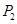 、
、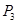 的坐标,从而使得
的坐标,从而使得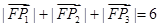 ;
;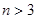 时,若
时,若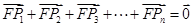 ,
, ;
;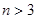 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即: ,则
,则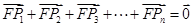 .”
.”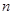 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com