
分析 利用三角恒等变换化简函数的解析式,再利用余弦函数的周期性以及它的图象的对称性,得出结论.
解答 解:函数$f(x)=2{cos^2}x+cos(2x+\frac{π}{3})-1$
=cos2x+cos2xcos$\frac{π}{3}$-sin2xsin$\frac{π}{3}$=$\frac{3}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x=$\sqrt{3}$cos(2x+$\frac{π}{6}$),
则函数的最小正周期为$\frac{2π}{2}$=π.
令2x+$\frac{π}{6}$=kπ,求得x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,结合x在[0,π]内,
可得f(x)在[0,π]内的一条对称轴方程是x=$\frac{5π}{12}$,或 x=$\frac{11π}{12}$,
故答案为:π;$x=\frac{5π}{12}$或$x=\frac{11π}{12}$.
点评 本题主要考查三角恒等变换,余弦函数的周期性以及它的图象的对称性,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
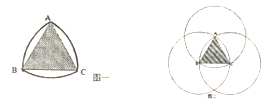 如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )
如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )| A. | $\frac{\sqrt{3}}{2π-\sqrt{3}}$ | B. | $\frac{\sqrt{3}}{2(π-\sqrt{3}})$ | C. | $\frac{2π-3\sqrt{3}}{2(π-\sqrt{3})}$ | D. | $\frac{2π-2\sqrt{3}}{2π-\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{10})$ | B. | $(\sqrt{10},+∞)$ | C. | $({1,\sqrt{10}}]$ | D. | $[{\sqrt{10}}\right.,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | ||
| C. | 4 | D. | 与点位置有关的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
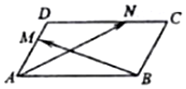 如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )
如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )| A. | [-3,1] | B. | [-3,-1] | C. | [-1,1] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 81π | B. | 16π | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com