
分析 分别求出两个函数的导函数,由两函数在切点处的导数相等,并由斜率公式,得到由此得到m=2n-2,则4n-4=aen有解.再由导数即可进一步求得a的取值.
解答 解:y=x2在点(m,m2)的切线斜率为2m,
y=aex在点(n,aen)的切线斜率为aen,
如果两个曲线存在公共切线,那么:2m=aen.
又由斜率公式得到,2m=$\frac{{m}^{2}-a{e}^{n}}{m-n}$,
由此得到m=2n-2,
则4n-4=aen有解.
由y=4x-4,y=aex的图象有交点即可.
设切点为(s,t),则aes=4,且t=4s-4=aes,
即有切点(2,4),a=$\frac{4}{{e}^{2}}$,
故a的取值范围是:a≤$\frac{4}{{e}^{2}}$且a≠0.
故答案为:(-∞,0)∪(0,$\frac{4}{{e}^{2}}$].
点评 本题考查利用导数研究曲线上某点的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,考查转化思想和运算能力,是中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
 中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a2>a1 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
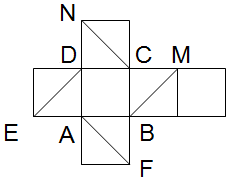 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4},\frac{1}{4},\frac{1}{2}$ | B. | $\frac{1}{4},\frac{1}{4},\frac{1}{4}$ | C. | $\frac{1}{3},\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{4},\frac{1}{3},\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不可能事件 | B. | 互斥但不对立事件 | ||
| C. | 对立事件 | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com