
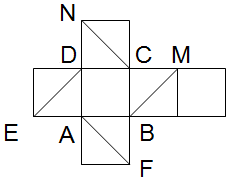
 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4). 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
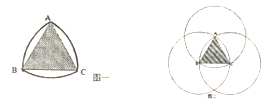 如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )
如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )| A. | $\frac{\sqrt{3}}{2π-\sqrt{3}}$ | B. | $\frac{\sqrt{3}}{2(π-\sqrt{3}})$ | C. | $\frac{2π-3\sqrt{3}}{2(π-\sqrt{3})}$ | D. | $\frac{2π-2\sqrt{3}}{2π-\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
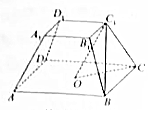 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
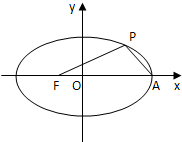 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
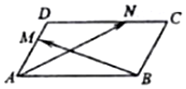 如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )
如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )| A. | [-3,1] | B. | [-3,-1] | C. | [-1,1] | D. | [1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com