
分析 利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用两角和差的三角公式化简f(x)+g(x)的解析式,再利用正弦函数的值域求得函数y=f(x)+g(x)的最大值.
解答 解:将函数f(x)=sinx的图象向右平移$\frac{π}{3}$个单位后得到函数y=g(x)=sin(x-$\frac{π}{3}$)的图象,
则函数y=f(x)+g(x)=sinx+sin(x-$\frac{π}{3}$)=$\frac{3}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx=$\sqrt{3}$sin(x-$\frac{π}{6}$) 的最大值为$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,两角和差的三角函数,正弦函数的值域,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {1} | C. | {0,1} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3i | B. | -3 | C. | 3i | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,$\frac{5}{2}$) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | (-$\frac{5}{2}$,$\frac{7}{2}$) | D. | ($\frac{5}{2}$,$\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4,5} | C. | {2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a2>a1 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
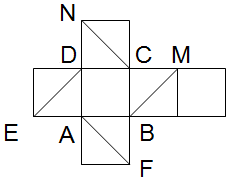 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com