
| A. | (-$\frac{3}{2}$,$\frac{5}{2}$) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | (-$\frac{5}{2}$,$\frac{7}{2}$) | D. | ($\frac{5}{2}$,$\frac{7}{2}$) |
分析 画出约束条件的可行域,利用目标函数的几何意义求解即可.
解答 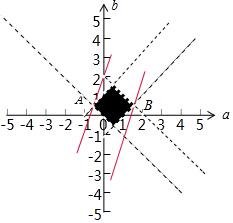 解:函数f(x)=ax+b,若0<f(1)<2,-1<f(-1)<1,
解:函数f(x)=ax+b,若0<f(1)<2,-1<f(-1)<1,
可得:$\left\{\begin{array}{l}{0<a+b<2}\\{-1<b-a<1}\end{array}\right.$的可行域如图:
令z=2a-b,结合可行域可知:z=2a-b经过A,B两点时,z取得最值,
由$\left\{\begin{array}{l}{a+b=0}\\{b-a=1}\end{array}\right.$可得A($-\frac{1}{2}$,$\frac{1}{2}$),
由$\left\{\begin{array}{l}{a+b=2}\\{b-a=-1}\end{array}\right.$可得B($\frac{3}{2}$,$\frac{1}{2}$),
2a-b的最大值为:3-$\frac{1}{2}$=$\frac{5}{2}$,
最小值为:$-1-\frac{1}{2}$=-$\frac{3}{2}$.
因为A,B都不在可行域,所以2a-b的范围是($-\frac{3}{2}$,$\frac{5}{2}$).
故选:A.
点评 本题考查线性规划的应用,考查转化思想数形结合思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$ | B. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | ||
| C. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | D. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
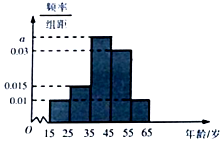 2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示:
2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示:| 关注民生 | 不关注民生 | 合计 | |
| 青少年组 | 90 | 30 | 120 |
| 中老年组 | 70 | 10 | 80 |
| 合计 | 160 | 40 | 200 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
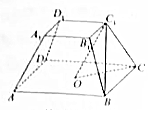 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com