
分析 (Ⅰ)求出C1和C2的直角坐标方程,得出交点坐标,再求C1和C2交点的极坐标;
(Ⅱ)利用参数的几何意义,即可求|PA|+|PB|.
解答 解:(Ⅰ)由C1,C2极坐标方程分别为ρ=2sinθ,$ρcos({θ-\frac{π}{4}})=\sqrt{2}$’
化为平面直角坐标系方程分为x2+(y-1)2=1,x+y-2=0. …(1分)
得交点坐标为(0,2),(1,1). …(3分)
即C1和C2交点的极坐标分别为$({2,\frac{π}{2}})\;\;({\sqrt{2},\frac{π}{4}})$.…(5分)
(II)把直线l的参数方程:$\left\{\begin{array}{l}x=-\sqrt{3}+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$(t为参数),代入x2+(y-1)2=1,
得${({-\sqrt{3}+\frac{{\sqrt{3}}}{2}t})^2}+{({\frac{1}{2}t-1})^2}=1$,…(7分)
即t2-4t+3=0,t1+t2=4,…(9分)
所以|PA|+|PB|=4.…(10分)
点评 本题考查极坐标方程转化为直角坐标方程,考查参数几何意义的运用,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:填空题
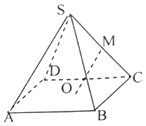 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
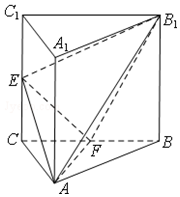 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com