
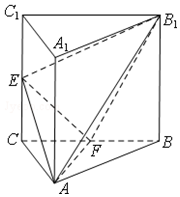
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.分析 (1)连结AF,由已知条件推导出面ABC⊥面BB1C1C,从而AF⊥B1F,由勾股定理得B1F⊥EF.由此能证明平面AB1F⊥平面AEF.
(2)利用等面积方法,即可求出点C到平面AEF的距离.
解答 (1)证明:连结AF,∵F是等腰直角三角形△ABC斜边BC的中点,
∴AF⊥BC.
又∵三棱柱ABC-A1B1C1为直三棱柱,
∴面ABC⊥面BB1C1C,
∴AF⊥面BB1C1C,AF⊥B1F.…(2分)
设AB=AA1=1,则B1F=$\frac{\sqrt{6}}{2}$,EF=$\frac{\sqrt{3}}{2}$,B1E=$\frac{3}{2}$.
∴B1F2+EF2=B1E2,∴B1F⊥EF.
又AF∩EF=F,∴B1F⊥平面AEF.…(4分)
而B1F?面AB1F,故:平面AB1F⊥平面AEF.…(5分)
(2)解:设点C到平面AEF的距离为h,则由题意,AF⊥CF,AF⊥EF,
∴S△ACF=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1,S△AEF=$\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{6}}{2}$,
由等体积可得,$\frac{1}{3}×1×1=\frac{1}{3}×\frac{\sqrt{6}}{2}h$,∴h=$\frac{\sqrt{6}}{3}$.
点评 本题考查平面与平面垂直的证明,考查点C到平面AEF的距离的求法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4,5} | C. | {2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a2>a1 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | p | $\frac{1}{3}$ | q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com