
| Ͷ�ʽ�� | ���� | ���ⲻ | ���� |
| ���� | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| Ͷ�ʽ�� | ���� | ���ⲻ | ���� |
| ���� | p | $\frac{1}{3}$ | q |
���� ��������֪��$p+\frac{1}{3}+q=1$��$p=\frac{1}{2}$���ɴ������$q=\frac{1}{6}$��
�����ɡ�������𡱿���ĸ��ʱȡ�Ͷ�ʹ��С�����ĸ���С����$q��\frac{3}{8}$����$p+\frac{1}{3}+q=1$��$p+\frac{1}{3}+q=1$��q��0�������p��ȡֵ��Χ��
�����¼�AΪ��һ�����ʦ������ʦ��������������һ�˻���������a��b��c�ֱ��ʾһ�����ʦ��������𡰻������������ⲻ���������𡱣���x��y��z�ֱ��ʾһ�����ʦ��������𡰻������������ⲻ���������𡱣��ɴ������оٷ��������һ�����ʦ������ʦ��������������һ�˻����ĸ��ʣ�
��� �⣺������Ϊ��������𡱺�Ͷ�ʽ��ֻ�С��������������ⲻ�������������֣�������Ͷ�ʽ���������
����$p+\frac{1}{3}+q=1$������Ϊ$p=\frac{1}{2}$������$q=\frac{1}{6}$��
�����ɡ�������𡱿���ĸ��ʱȡ�Ͷ�ʹ��С�����ĸ���С����$q��\frac{3}{8}$��
��Ϊ$p+\frac{1}{3}+q=1$��
����$q=\frac{2}{3}-p��\frac{3}{8}$�����$p��\frac{7}{24}$��
����Ϊ$p+\frac{1}{3}+q=1$��q��0��
����$p��\frac{2}{3}$��
����$\frac{7}{24}��p��\frac{2}{3}$��
�����¼�AΪ��һ�����ʦ������ʦ��������������һ�˻�������
��a��b��c�ֱ��ʾһ�����ʦ��������𡰻������������ⲻ���������𡱣���x��y��z�ֱ��ʾһ�����ʦ��������𡰻������������ⲻ���������𡱣�
��һ�����ʦ������ʦ������������п��ܵ�Ͷ�ʽ����3��3=9�֣������ǣ���a��x������a��y������a��z������b��x������b��y������b��z������c��y������c��z����
�����¼�A�Ľ����5�֣������ǣ���a��x������a��y������a��z������b��x������c��x����
�����һ�����ʦ������ʦ��������������һ�˻����ĸ���$P��A��=\frac{5}{9}$��
���� ���⿼����ʵ���Ӧ�ã��ǻ����⣬����ʱҪ�������⣬ע��ȿ����¼����ʹ�ʽ���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 4 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�������x���ϵ���ԲC��$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1�����㣨b��2e��������eΪ��ԲC�������ʣ�����T��1��0����б��Ϊk��k��0����ֱ��l����ԲC��A��B���㣨A��x���·�����
��ͼ����ƽ��ֱ������ϵxOy�У�������x���ϵ���ԲC��$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1�����㣨b��2e��������eΪ��ԲC�������ʣ�����T��1��0����б��Ϊk��k��0����ֱ��l����ԲC��A��B���㣨A��x���·������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
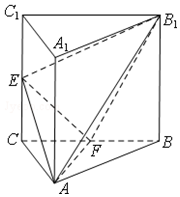 ��ͼ��������ABC-A1B1C1�У�����AA1��ƽ��ABC����ABCΪ����ֱ�������Σ���BAC=90�㣬��AA1=AB=2��E��F�ֱ���CC1��BC���е㣮
��ͼ��������ABC-A1B1C1�У�����AA1��ƽ��ABC����ABCΪ����ֱ�������Σ���BAC=90�㣬��AA1=AB=2��E��F�ֱ���CC1��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
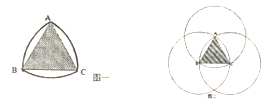 ��ͼһ��ʾ���ɻ�AB����AC����BC����ɵ�ͼ�ν������������Σ����ɵ¹���е����ר�ҡ���е�˶�ѧ���������ȷ��ֵģ����Ĺ�����ͼ����ʾ������������ABCd��ÿ������ΪԲ�ģ��Ա߳�Ϊ�뾶�����������������һ�λ��������λ���Χ�ɵ����������μ�Ϊ���������Σ���һ����ͼһ��ʾ�İ��ӣ�ij����������һ�������˼�һ�������а��������а����е�����һ���ǵȿ��ܵģ���˼�ǡ������������ABC�ڲ�������Ӱ���֣��ĸ���Ϊ��������
��ͼһ��ʾ���ɻ�AB����AC����BC����ɵ�ͼ�ν������������Σ����ɵ¹���е����ר�ҡ���е�˶�ѧ���������ȷ��ֵģ����Ĺ�����ͼ����ʾ������������ABCd��ÿ������ΪԲ�ģ��Ա߳�Ϊ�뾶�����������������һ�λ��������λ���Χ�ɵ����������μ�Ϊ���������Σ���һ����ͼһ��ʾ�İ��ӣ�ij����������һ�������˼�һ�������а��������а����е�����һ���ǵȿ��ܵģ���˼�ǡ������������ABC�ڲ�������Ӱ���֣��ĸ���Ϊ��������| A�� | $\frac{\sqrt{3}}{2��-\sqrt{3}}$ | B�� | $\frac{\sqrt{3}}{2����-\sqrt{3}}��$ | C�� | $\frac{2��-3\sqrt{3}}{2����-\sqrt{3}��}$ | D�� | $\frac{2��-2\sqrt{3}}{2��-\sqrt{3}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
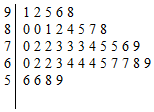 �й�ʫ�ʴ��IJ���������ȫ��Ķ����ȣ�ijСѧ������ʦ�ڰ��↑չ��һ��ʫ��Ĭд����������40��ѧ���÷����ݵľ�Ҷͼ��ͼ��ʾ�����涨�÷ֲ�С��85�ֵ�ѧ���õ���ʫ�ʴ��ˡ��ijƺţ�С��85���Ҳ�С��70�ֵ�ѧ���õ���ʫ�����֡��ijƺţ�����ѧ���õ���ʫ�ʰ����ߡ��ijƺţ����ݸôα����ijɾͰ��ճƺŵIJ�ͬ���зֲ������ѡ10��ѧ�������ѡ��ѧ���л�á�ʫ�����֡��ƺŵ�����Ϊ��������
�й�ʫ�ʴ��IJ���������ȫ��Ķ����ȣ�ijСѧ������ʦ�ڰ��↑չ��һ��ʫ��Ĭд����������40��ѧ���÷����ݵľ�Ҷͼ��ͼ��ʾ�����涨�÷ֲ�С��85�ֵ�ѧ���õ���ʫ�ʴ��ˡ��ijƺţ�С��85���Ҳ�С��70�ֵ�ѧ���õ���ʫ�����֡��ijƺţ�����ѧ���õ���ʫ�ʰ����ߡ��ijƺţ����ݸôα����ijɾͰ��ճƺŵIJ�ͬ���зֲ������ѡ10��ѧ�������ѡ��ѧ���л�á�ʫ�����֡��ƺŵ�����Ϊ��������| A�� | 2 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��1��\sqrt{10}��$ | B�� | $��\sqrt{10}��+�ޣ�$ | C�� | $��{1��\sqrt{10}}]$ | D�� | $[{\sqrt{10}}\right.��+�ޣ�$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com