
分析 (Ⅰ)由已知结合正弦定理,求出tanA的值,从而求出A的值;
(II)由A化简函数f(x)为正弦型函数,求出x∈[0,$\frac{π}{2}$]时f(x)的值域.
解答 解:(Ⅰ)△ABC中,bsin2A=$\sqrt{3}$acosAsinB,
由正弦定理得,sinBsin2A=$\sqrt{3}$sinAcosAsinB,
∴tanA=$\frac{sinA}{cosA}$=$\sqrt{3}$,…(2分)
又A∈(0,π),
∴$A=\frac{π}{3}$;…(4分)
(II)由A=$\frac{π}{3}$,
∴函数f(x)=sinAcos2x-sin2$\frac{A}{2}$sin 2x
=$\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sinxcosx
=$\frac{\sqrt{3}}{2}$•$\frac{1+cos2x}{2}$-$\frac{1}{2}$•$\frac{1}{2}$sin2x
=-$\frac{1}{2}$($\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x)+$\frac{\sqrt{3}}{4}$,
=-$\frac{1}{2}$sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{4}$,
∵x∈[0,$\frac{π}{2}$],∴-$\frac{π}{3}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$,…(10分)
∴-$\frac{\sqrt{3}}{2}$≤sin(2x-$\frac{π}{3}$)≤1,
∴$\frac{\sqrt{3}-2}{4}$≤-$\frac{1}{2}$sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{4}$≤$\frac{\sqrt{3}}{2}$,
所以f(x)的值域为$[{\frac{{\sqrt{3}-2}}{4},\frac{{\sqrt{3}}}{2}}]$.…(12分)
点评 本题考查了正弦定理以及三角函数的图象与性质的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | m⊥l,m?α | B. | m⊥l,m∥α | C. | m∥l,m∩α≠∅ | D. | m⊥l,m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
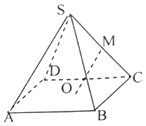 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
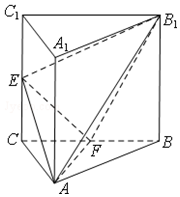 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com