
分析 根据等差数列和等比数列的求和公式计算即可.
解答 解:设首项为a,
则an=a•2n-1,
∴bn=log2an=log2a+n-1
∴bn-bn-1=log2an-log2an-1=log22=1,
∴数列{bn}是以log2a为首项,以1为公差的等差数列,
∴10log2a+$\frac{10×(10-1)}{2}$=25,
∴a=$\frac{1}{4}$
∴数列{an}的首项为$\frac{1}{4}$,
∴a1+a2+a3+…+a10=$\frac{\frac{1}{4}(1-{2}^{10})}{1-2}$=$\frac{1023}{4}$,
故答案为:$\frac{1023}{4}$
点评 本题考查了等差数列和等比数列的求和公式,属于基础题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
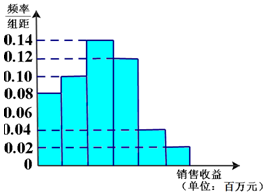 简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {1} | C. | {0,1} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3i | B. | -3 | C. | 3i | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4,5} | C. | {2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com