
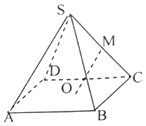
 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$. 分析 连接DB,取SD的中点N,连接ON,MN,OC,则ON∥SB,∠MON是异面直线OM与SB所成角,求出三角形的三边,利用余弦定理,可得结论.
解答 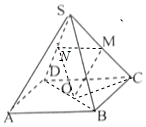 解:连接DB,取SD的中点N,连接ON,MN,OC,则ON∥SB,
解:连接DB,取SD的中点N,连接ON,MN,OC,则ON∥SB,
∴∠MON是异面直线OM与SB所成角,
又cos∠SCO=$\frac{1}{2}$,∠SCO=60°
∴OM=1,
∵ON=1,MN=$\frac{\sqrt{2}}{2}$,
∴cos∠MON=$\frac{1+1-\frac{1}{2}}{2×1×1}$=$\frac{3}{4}$,
故答案为$\frac{3}{4}$.
点评 本题考查异面直线OM与SB所成角的余弦值,考查余弦定理的运用,正确找出异面直线OM与SB所成角是关键.


科目:高中数学 来源: 题型:选择题
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为| A. | $\frac{19}{3}$ | B. | $\frac{53}{8}$ | C. | $\frac{171}{6}$ | D. | $\frac{185}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
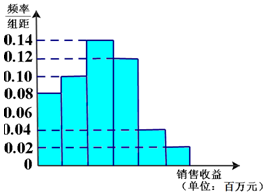 简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {1} | C. | {0,1} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com