
分析 (Ⅰ)利用列举法能写出这个试验的所有基本事件.
(Ⅱ)记“恰有一枚正面向上”为事件A,事件A所包含的基本事件数为3,由此能求出事件“恰有一枚正面向上”的概率.
(Ⅲ)记“至少有两枚正面向上”为事件B,则事件B所包含的基本事件数为4,由此能求出事件“至少有两枚正面向上”的概率.
解答 解:(Ⅰ)这个试验的基本事件为:
(正,正,正),(正,正,反),(正,反,正),(正,反,反),(反,正,正),
(反,正,反),(反,反,正),(反,反,反),共8个.…3分
(Ⅱ)记“恰有一枚正面向上”为事件A,
则事件A所包含的基本事件数为3,
所以事件“恰有一枚正面向上”的概率$P(A)=\frac{3}{8}$.…6分
(Ⅲ)记“至少有两枚正面向上”为事件B,
则事件B所包含的基本事件数为4,
所以事件“至少有两枚正面向上”的概率$P(B)=\frac{4}{8}=\frac{1}{2}$.…9分.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
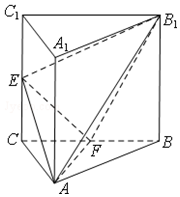 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{10})$ | B. | $(\sqrt{10},+∞)$ | C. | $({1,\sqrt{10}}]$ | D. | $[{\sqrt{10}}\right.,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com