
| A. | $\frac{1}{4},\frac{1}{4},\frac{1}{2}$ | B. | $\frac{1}{4},\frac{1}{4},\frac{1}{4}$ | C. | $\frac{1}{3},\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{4},\frac{1}{3},\frac{1}{2}$ |
分析 利用等可能事件概率计算公式、相互独立事件概率乘法公式,互斥事件概率加法公式求解.
解答 解:从标有1、2、3、4的卡片中不放回地先后抽出两张卡片,
则4号卡片“第一次被抽到的概率”p1=$\frac{1}{4}$,
“第二次被抽到的概率”${p}_{2}=\frac{3}{4}×\frac{1}{3}=\frac{1}{4}$,
“在整个抽样过程中被抽到的概率”p3=$\frac{1}{4}+\frac{3}{4}×\frac{1}{4}$=$\frac{1}{2}$.
故选:A.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式、相互独立事件概率乘法公式,互斥事件概率加法公式的合理运用.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
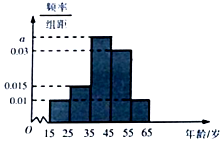 2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示:
2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示:| 关注民生 | 不关注民生 | 合计 | |
| 青少年组 | 90 | 30 | 120 |
| 中老年组 | 70 | 10 | 80 |
| 合计 | 160 | 40 | 200 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
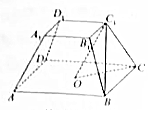 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
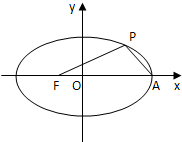 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | ||
| C. | 4 | D. | 与点位置有关的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com