
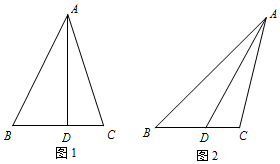
 如图,在△ABC中,D为边BC上一点,AD=6,BD=3,
如图,在△ABC中,D为边BC上一点,AD=6,BD=3,分析 (1)设∠BAD=α,∠DAC=β,由已知可求tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,利用两角和的正切函数公式可求tan∠BAC=1.结合范围∠BAC∈(0,π),即可得解∠BAC的值.
(2)设∠BAD=α.由正弦定理可求sinα=$\frac{\sqrt{2}}{4}$,利用大边对大角,同角三角函数基本关系式可求cosα的值,利用两角和的正弦函数公式可求sin∠ADC,进而利用三角形面积公式即可计算得解.
解答 (本小题满分14分)
解:(1)设∠BAD=α,∠DAC=β.
因为AD⊥BC,AD=6,BD=3,DC=2,
所以tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,…(2分)
所以tan∠BAC=tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=1.…(4分)
又∠BAC∈(0,π),
所以∠BAC=$\frac{π}{4}$.…(6分)
(2)设∠BAD=α.在△ABD中,∠ABC=$\frac{π}{4}$,AD=6,BD=3.
由正弦定理得$\frac{AD}{sin\frac{π}{4}}$=$\frac{BD}{sinα}$,解得sinα=$\frac{\sqrt{2}}{4}$.…(8分)
因为AD>BD,
所以α为锐角,从而cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{\sqrt{14}}{4}$.…(10分)
因此sin∠ADC=sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{4}$+$\frac{\sqrt{14}}{4}$)=$\frac{1+\sqrt{7}}{4}$.…(12分)
△ADC的面积S=$\frac{1}{2}$×AD×DC•sin∠ADC=$\frac{1}{2}$×6×2×$\frac{1+\sqrt{7}}{4}$=$\frac{3}{2}$(1+$\sqrt{7}$).…(14分)
点评 本题主要考查了两角和的正切函数公式,正弦定理,大边对大角,同角三角函数基本关系式,两角和的正弦函数公式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (-∞,e] | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校为指导学生合理选择文理科的学习,根据数理综合测评成绩,按6分为满分进行折算后,若学生成绩小于m分别建议选择文科,不低于m分则建议选择理科(这部分学生称为候选理科生).现从该校高一随机抽取500名学生的数理综合成绩作为样本,整理得到分数的频率分布直方图(如图所示).
某校为指导学生合理选择文理科的学习,根据数理综合测评成绩,按6分为满分进行折算后,若学生成绩小于m分别建议选择文科,不低于m分则建议选择理科(这部分学生称为候选理科生).现从该校高一随机抽取500名学生的数理综合成绩作为样本,整理得到分数的频率分布直方图(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com