
分析 (1)求出直线l的方程,与椭圆方程联立借助韦达定理及弦长公式求弦长|AB|的值.
(2)∠AOB为锐角,针对本题它等价于$\overrightarrow{OA}•\overrightarrow{OB}$>0,确定b=2-$\frac{{k}^{2}}{4}$,y=kx+b代入$\frac{{x}^{2}}{2}$+y2=1,整理可得(2+k2)x2+4kbx+2b2-2=0,利用韦达定理,即可得出结论.
解答 解:(1)根据l的斜率为2,可知y′=2x=2,∴x=1,
所以P(1,3),所以直线l的方程为y-3=2(x-1),即2x-y+1=0.
与椭圆C1:$\frac{{x}^{2}}{2}$+y2=1联立,可得9x2+8x=0,
∴x=0或-$\frac{8}{9}$,
∴|AB|=$\sqrt{1+4}•\frac{8}{9}$=$\frac{8\sqrt{5}}{9}$;
(2)设A(x1,y1),B(x2,y2),切点(x0,y0),
∠AOB为锐角,针对本题它等价于$\overrightarrow{OA}•\overrightarrow{OB}$>0,
即x1x2+y1y2>0,x1x2+(kx1+b)(kx2+b)>0,
再根据k=2x0,∴x0=$\frac{k}{2}$,y0=$\frac{{k}^{2}}{4}$+2,
∴$\frac{{k}^{2}}{4}$+2=k•$\frac{k}{2}$+b,
∴b=2-$\frac{{k}^{2}}{4}$,①
y=kx+b代入$\frac{{x}^{2}}{2}$+y2=1,整理可得(2+k2)x2+4kbx+2b2-2=0,
∴x1+x2=-$\frac{4kb}{2+{k}^{2}}$,x1x2=$\frac{2{b}^{2}-2}{2+{k}^{2}}$,△>0②
∴y1y2=(kx1+b)(kx2+b)=$\frac{2{b}^{2}-2{k}^{2}}{2+{k}^{2}}$,
∴$\frac{2{b}^{2}-2}{2+{k}^{2}}$+$\frac{2{b}^{2}-2{k}^{2}}{2+{k}^{2}}$>0③,
由①②③解得b∈(-4-$\sqrt{33}$,$\frac{-4-\sqrt{70}}{3}$)∪($\frac{-4+\sqrt{70}}{3}$,-4+$\sqrt{33}$).
点评 本题考查圆锥曲线的综合问题,考查直线与抛物线、椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -2<x<6 | B. | -1<x≤5 | C. | -2<x<-1 | D. | -1<x<5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
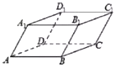 如图,在平行六面体ABCD-A1B1C1D1中,AA1=AB=AD=$\sqrt{3}$,若∠A1AD=∠A1AB=45°,∠BAD=60°,则点A1到平面ABCD的距离为( )
如图,在平行六面体ABCD-A1B1C1D1中,AA1=AB=AD=$\sqrt{3}$,若∠A1AD=∠A1AB=45°,∠BAD=60°,则点A1到平面ABCD的距离为( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 5$\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com