
分析 过A作AO⊥BD,交BD于O,连结A′O,由AA′⊥平面BCD,知∠AOA′是二面角A-BD-C的平面角,由此能求出二面角A-BD-C的余弦值.
解答 解:∵过A作AO⊥BD,交BD于O,连结A′O,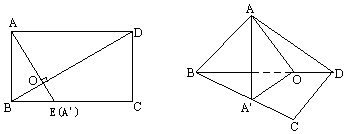
∵沿对角线BD把△ABD折起,使点A在平面BCD上的射影A′落在BC上,
∴AA′⊥平面BCD,∴∠AOA′是二面角A-BD-C的平面角,
∵矩形ABCD中,AB=3,BC=4,
∴AO=$\frac{AB•AD}{BD}$=$\frac{12}{5}$,BO=$\frac{A{B}^{2}}{BD}=\frac{9}{5}$,tan$∠CBD=\frac{CD}{BC}$=$\frac{3}{4}$,
A′O=OE=BO•tan∠CBD=$\frac{9}{5}•\frac{3}{4}$=$\frac{27}{20}$,
在Rt△AA′O中,∠AA′O=90°,
∴$cos∠AO{A}^{'}=\frac{A{O}^{'}}{AO}=\frac{9}{16}$,
∴二面角A-BD-C的余弦值为$\frac{9}{16}$.
故答案为:$\frac{9}{16}$.
点评 本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{3}{4}-6ln\frac{3}{2},2-6ln2)$ | B. | (2-6ln2,+∞) | ||
| C. | $(-\frac{3}{4}-6ln\frac{3}{2},6ln2-2)$ | D. | (-∞,6ln2-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
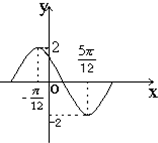 函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)在一个周期内的图象如图所示,为了得到y=2sin2x的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)在一个周期内的图象如图所示,为了得到y=2sin2x的图象,只需将f(x)的图象( )| A. | 向右平移$\frac{5π}{6}$个单位长度 | B. | 向左平移$\frac{5π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向左平移$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com