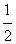解:(1)∵A=[-1,1],B=[-

,

],C⊆A∪B=A,二次函数f(x)=2x
2+mx-1图象开口向上,且△=m
2+8>0恒成立,
故图象始终与x轴有两个交点,由题意,要使这两个交点横坐标x
1,x
2∈[-1,1],当且仅当:

,…(4分),解得:-1≤m≤1 …(5分)
(2)对任意x∈R都有f(1+x)=f(1-x),所以f(x)象关于直线x=1对称,所以-

=1,得m=-4.(7分)
所以f(x)=2(x-1)
2-3为[-

,

]上减函数.f(x)
min=-2

;f(x)
max=2

.故x∈B时,f(x)值域为[-2

,2

].…(9分)
(3)令φ(x)=f(x)+g(x),则φ(x)=x
2+|x-a|-1,
(i)当x≤a时,φ(x)=x
2-x+a-1=

+a-

,
当a≤

,则函数φ(x)在(-∞,a]上单调递减,从而函数φ(x)在(-∞,a]上的最小值为φ(a)=a
2-1.
若a>

,则函数φ(x)在(-∞,a]上的最小值为φ(

)=-

+a,且φ(-

)≤φ(a).(12分)
(ii)当x≥a时,函数φ(x)=x
2+x-a-1=

-a-

,
若a≤-

,则函数φ(x)在(-∞,a]上的最小值为φ(-

)=-

-a,且φ(-

)≤φ(a),
若a>-

,则函数φ(x)在[a,+∞)上单调递增,
从而函数φ(x)在[a,+∞)上的最小值为φ(a)=a
2-1.…(15分)
综上,当a≤-

时,函数φ(x)的最小值为-

-a,当-

<a≤

时,函数φ(x)的最小值为a
2-1;当a>

时,函数φ(x)的最小值为-

+a. …(16分)
分析:(1)依题意,C⊆A∪B=A=[-1,1],二次函数f(x)=2x
2+mx-1图象开口向上,且△=m
2+8>0恒成立,图象始终与x轴有两个交点?

,从而可求得实数m取值范围;
(2)由于f(x)象关于直线x=1对称,可得m=-4,由f(x)=2(x-1)
2-3为[-

,

]上减函数可求得x∈B时,f(x)的值域;
(3)令φ(x)=f(x)+g(x),则φ(x)=x
2+|x-a|-1,分x≤a与x≥a先去掉绝对值符号,再根据其对称轴对a分类讨论,利用函数的单调性即可求得答案.
点评:本题考查带绝对值的函数,考查集合关系中的参数取值问题,突出考查二次函数的性质,考查综合分析与运算能力,考查分类讨论思想,化归思想,方程思想的运用,属于难题.

 ,
, ],函数f(x)=2x2+mx-1.
],函数f(x)=2x2+mx-1. ,
, ],C⊆A∪B=A,二次函数f(x)=2x2+mx-1图象开口向上,且△=m2+8>0恒成立,
],C⊆A∪B=A,二次函数f(x)=2x2+mx-1图象开口向上,且△=m2+8>0恒成立, ,…(4分),解得:-1≤m≤1 …(5分)
,…(4分),解得:-1≤m≤1 …(5分) =1,得m=-4.(7分)
=1,得m=-4.(7分) ,
, ]上减函数.f(x)min=-2
]上减函数.f(x)min=-2 ;f(x)max=2
;f(x)max=2 .故x∈B时,f(x)值域为[-2
.故x∈B时,f(x)值域为[-2 ,2
,2 ].…(9分)
].…(9分) +a-
+a- ,
, ,则函数φ(x)在(-∞,a]上单调递减,从而函数φ(x)在(-∞,a]上的最小值为φ(a)=a2-1.
,则函数φ(x)在(-∞,a]上单调递减,从而函数φ(x)在(-∞,a]上的最小值为φ(a)=a2-1. ,则函数φ(x)在(-∞,a]上的最小值为φ(
,则函数φ(x)在(-∞,a]上的最小值为φ( )=-
)=- +a,且φ(-
+a,且φ(- )≤φ(a).(12分)
)≤φ(a).(12分) -a-
-a- ,
, ,则函数φ(x)在(-∞,a]上的最小值为φ(-
,则函数φ(x)在(-∞,a]上的最小值为φ(- )=-
)=- -a,且φ(-
-a,且φ(- )≤φ(a),
)≤φ(a), ,则函数φ(x)在[a,+∞)上单调递增,
,则函数φ(x)在[a,+∞)上单调递增, 时,函数φ(x)的最小值为-
时,函数φ(x)的最小值为- -a,当-
-a,当- <a≤
<a≤ 时,函数φ(x)的最小值为a2-1;当a>
时,函数φ(x)的最小值为a2-1;当a> 时,函数φ(x)的最小值为-
时,函数φ(x)的最小值为- +a. …(16分)
+a. …(16分) ,从而可求得实数m取值范围;
,从而可求得实数m取值范围; ,
, ]上减函数可求得x∈B时,f(x)的值域;
]上减函数可求得x∈B时,f(x)的值域;

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案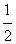 ,3},则使函数y=xa的定义域为R且为奇函数的所有a的值是
,3},则使函数y=xa的定义域为R且为奇函数的所有a的值是