
已知等差数列{ }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设 =
= ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.
(1)an=n+1;(2)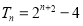 .
.
【解析】
试题分析:本题主要考查等差数列的通项公式、等比数列的通项公式、等差数列的前n项和公式、等比数列的前n项和公式、等比中项等数学知识,考查学生的分析问题的能力和计算能力.第一问,先利用等比中项写出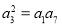 ,再用等差数列的通项公式将
,再用等差数列的通项公式将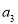 和
和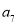 展开,用等差数列的前n项和将
展开,用等差数列的前n项和将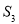 展开,两式联立,求出
展开,两式联立,求出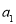 和
和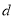 ,再写出通项公式即可;第二问,将第一问的结果代入,化简
,再写出通项公式即可;第二问,将第一问的结果代入,化简 表达式,利用等比数列的定义证明
表达式,利用等比数列的定义证明 为等比数列,再利用等比数列的前n项和公式计算
为等比数列,再利用等比数列的前n项和公式计算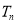 .
.
试题解析:(1) 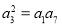 ,即(a1+2d)2=a1(a1+6d),化简得
,即(a1+2d)2=a1(a1+6d),化简得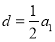 ,d=0(舍去).
,d=0(舍去).
∴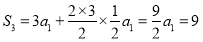 ,得a1=2,d=1.
,得a1=2,d=1.
∴an=a1+(n-1)d=2+(n-1)=n+1,即an=n+1.(6分)
(2)∵bn=2an=2n+1,∴b1=4,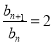 .
.
∴{bn}是以4为首项,2为公比的等比数列,
∴ .(12分)
.(12分)
考点:1.等比中项;2.等差数列的通项公式;3.等差数列的前n项和公式;4.等比数列的定义;5.等比数列的前n项和.


科目:高中数学 来源:2014-2015学年黑龙江省高一上第一次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)已知二次函数f(x)满足条件: ,
,
(1)求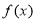 ;
;
(2)讨论二次函数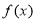 在闭区间
在闭区间 (
( )上的最小值.
)上的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
如图,设圆弧 与两坐标轴正半轴围成的扇形区域为
与两坐标轴正半轴围成的扇形区域为 ,过圆弧上一点
,过圆弧上一点 做该圆的切线与两坐标轴正半轴围成的三角形区域为
做该圆的切线与两坐标轴正半轴围成的三角形区域为 .现随机在区域
.现随机在区域 内投一点
内投一点 ,若设点
,若设点 落在
落在
区域 内的概率为
内的概率为 ,则
,则 的最大值为( )
的最大值为( )
A. B.
B. C.
C. D.
D.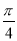

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com