
ЁОЬтФПЁПЮЊСЫНтдЫЖЏНЁЩэМѕЗЪЕФаЇЙћЃЌФГНЁЩэЗПЕїВщСЫ20УћЗЪХжепЃЌНЁЩэжЎЧАЫћУЧЕФЬхжиЧщПіШчШ§ЮЌБ§ЭМЃЈ1ЃЉЫљЪОЃЌОЙ§ЫФИідТЕФНЁЩэКѓЃЌЫћУЧЕФЬхжиЧщПіШчШ§ЮЌБ§ЭМЃЈ2ЃЉЫљЪОЃЎЖдБШНЁЩэЧАКѓЃЌЙигкет20УћЗЪХжепЃЌЯТУцНсТлВЛе§ШЗЕФЪЧЃЈ ЃЉ
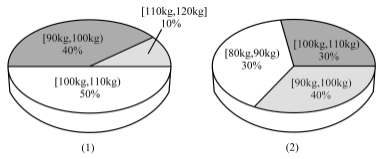
A.ЫћУЧНЁЩэКѓЃЌЬхжидкЧјМф[90kgЃЌ100kgЃЉФкЕФШЫЪ§ВЛБф
B.ЫћУЧНЁЩэКѓЃЌЬхжидкЧјМф[100kgЃЌ110kgЃЉФкЕФШЫЪ§МѕЩйСЫ4ШЫ
C.ЫћУЧНЁЩэКѓЃЌет20ЮЛНЁЩэепЬхжиЕФжаЮЛЪ§ЮЛгк[90kgЃЌ100kgЃЉ
D.ЫћУЧНЁЩэКѓЃЌдРДЬхжидк[110kgЃЌ120kg]ФкЕФЗЪХжепЬхжиЖМжСЩйМѕЧсСЫ10kg
ЁОД№АИЁПD
ЁОНтЮіЁП
ИљОнБ§ЭМж№ИібЁЯюМЦЫуЗжЮіМДПЩ.
ЖдA,взЕУУЧНЁЩэКѓ,ЬхжидкЧјМф[90kg,100kgЃЉФкЕФШЫЪ§еМБШОљЮЊ![]() ,ЙЪAе§ШЗ.
,ЙЪAе§ШЗ.
ЖдB,ЬхжидкЧјМф[100kg,110kgЃЉФкЕФШЫЪ§МѕЩйСЫ![]() ,МД
,МД![]() ШЫ.
ШЫ.
ЙЪBе§ШЗ.
ЖдC,вђЮЊНЁЩэКѓ[80kg,90kgЃЉФкЕФШЫЪ§еМ![]() ,[90kg,100kgЃЉФкЕФШЫЪ§еМ
,[90kg,100kgЃЉФкЕФШЫЪ§еМ![]() ,ЙЪжаЮЛЪ§ЮЛгк[90kg,100kgЃЉ.ЙЪCе§ШЗ.
,ЙЪжаЮЛЪ§ЮЛгк[90kg,100kgЃЉ.ЙЪCе§ШЗ.
ЖдD,взОйГіЗДР§ШєдЬхжидк[110kg,120kg]ФкЕФЗЪХжепжиСПЮЊ![]() ,МѕЗЪКѓЮЊ
,МѕЗЪКѓЮЊ![]() вРШЛТњзу.ЙЪDДэЮѓ.
вРШЛТњзу.ЙЪDДэЮѓ.
ЙЪбЁЃКD


 КЫаФЫибјбЇСЗЦРЯЕСаД№АИ
КЫаФЫибјбЇСЗЦРЯЕСаД№АИ ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ
ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌвбжЊЧњЯп
жаЃЌвбжЊЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭжБЯп
ЕФЦеЭЈЗНГЬКЭжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЩфЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЃЉ.Щш
ЃЉ.Щш![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЕФЕМКЏЪ§
ЕФЕМКЏЪ§![]() ЪЧХМКЏЪ§ЃЌШєЗНГЬ
ЪЧХМКЏЪ§ЃЌШєЗНГЬ![]() дкЧјМф
дкЧјМф![]() (Цфжа
(Цфжа![]() ЮЊздШЛЖдЪ§ЕФЕз)ЩЯгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђЪЕЪ§
ЮЊздШЛЖдЪ§ЕФЕз)ЩЯгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЩшКЏЪ§
ЪБЃЌЩшКЏЪ§![]() ЃЌШєДцдкЧјМф
ЃЌШєДцдкЧјМф![]() ЃЌЪЙЕУКЏЪ§
ЃЌЪЙЕУКЏЪ§![]() дк
дк![]() ЩЯЕФжЕгђЮЊ
ЩЯЕФжЕгђЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЖрУцЬх![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌ
ЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
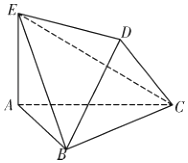
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩШёЖўУцНЧЕФгрЯвжЕЃЎ
ЫљГЩШёЖўУцНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§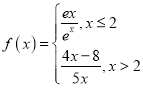 ЃЌЃЈЦфжаeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌШєЙигкxЕФЗНГЬ
ЃЌЃЈЦфжаeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌШєЙигкxЕФЗНГЬ![]() ЧЁга5ИіЯрвьЕФЪЕИљЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЮЊ________.
ЧЁга5ИіЯрвьЕФЪЕИљЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВЉРРЛсАВХХСЫЗжБ№БъгаађКХЮЊЁА1КХЁБЁА2КХЁБЁА3КХЁБЕФШ§СОГЕЃЌЕШПЩФмЫцЛњЫГађЧАЭљОЦЕъНгМЮБіЃЎФГМЮБіЭЛЗЂЦцЯыЃЌЩшМЦСНжжГЫГЕЗНАИЃЎЗНАИвЛЃКВЛГЫзјЕквЛСОГЕЃЌШєЕкЖўСОГЕЕФГЕађКХДѓгкЕквЛСОГЕЕФГЕађКХЃЌОЭГЫзјДЫГЕЃЌЗёдђГЫзјЕкШ§СОГЕЃЛЗНАИЖўЃКжБНгГЫзјЕквЛСОГЕЃЎМЧЗНАИвЛгыЗНАИЖўзјЕНЁА3КХЁБГЕЕФИХТЪЗжБ№ЮЊP1ЃЌP2ЃЌдђЃЈ ЃЉ
A. P1P2ЃН![]() B. P1ЃНP2ЃН
B. P1ЃНP2ЃН![]() C. P1+P2ЃН
C. P1+P2ЃН![]() D. P1ЃМP2
D. P1ЃМP2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇ2018ФъЕФИпПМПМЩњШЫЪ§ЪЧ2015ФъИпПМПМЩњШЫЪ§ЕФ![]() БЖЃЌЮЊСЫИќКУЕиЖдБШИУаЃПМЩњЕФЩ§бЇЧщПіЃЌЭГМЦСЫИУаЃ2015ФъКЭ2018ФъЕФИпПМЧщПіЃЌЕУЕНШчЭМжљзДЭМЃК
БЖЃЌЮЊСЫИќКУЕиЖдБШИУаЃПМЩњЕФЩ§бЇЧщПіЃЌЭГМЦСЫИУаЃ2015ФъКЭ2018ФъЕФИпПМЧщПіЃЌЕУЕНШчЭМжљзДЭМЃК

дђЯТСаНсТле§ШЗЕФЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. гы2015ФъЯрБШЃЌ2018ФъвЛБОДяЯпШЫЪ§МѕЩй
B. гы2015ФъЯрБШЃЌ2018ФъЖўБОДяЯпШЫЪ§діМгСЫ![]() БЖ
БЖ
C. 2015Фъгы2018ФъвеЬхДяЯпШЫЪ§ЯрЭЌ
D. гы2015ФъЯрБШЃЌ2018ФъВЛЩЯЯпЕФШЫЪ§гаЫљдіМг
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊЦНааЫФБпаЮЃЌЕуEдкABЩЯЃЌAEЃН2EBЃН2ЃЌЧвDEЁЭAB.вдDEЮЊелКлАбЁїADEелЦ№ЃЌЪЙЕуAЕНДяЕуFЕФЮЛжУЃЌЧвЁЯFEBЃН60Ёу.
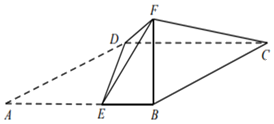
ЃЈ1ЃЉЧѓжЄЃКЦНУцBFCЁЭЦНУцBCDEЃЛ
ЃЈ2ЃЉШєжБЯпDFгыЦНУцBCDEЫљГЩНЧЕФе§ЧажЕЮЊ![]() ЃЌЧѓЖўУцНЧEЉDFЉCЕФе§ЯвжЕ.
ЃЌЧѓЖўУцНЧEЉDFЉCЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com