
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,设函数
时,设函数![]() ,若存在区间
,若存在区间![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)答案不唯一,见解析 (3)
(2)答案不唯一,见解析 (3)![]()
【解析】
(1)求导,接着单调区间,即可得出最小值;
(2)求导,对![]() 分类讨论,可求出函数
分类讨论,可求出函数![]() 的单调区间;
的单调区间;
(3)求出![]() ,通过分析
,通过分析![]() ,可得到
,可得到![]() 在
在![]() 增函数,从而有
增函数,从而有![]() ,转化为
,转化为![]() 在
在![]() 上至少有两个不同的正根
上至少有两个不同的正根![]() ,
,![]() ,转化为
,转化为![]() 与
与![]()
![]() 至少有两个交点,即可求出实数
至少有两个交点,即可求出实数![]() 的最大值.
的最大值.
(1)当![]() 时,
时,![]() ,
,
这时的导数![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() 得到
得到![]() ,
,
令![]() 得到
得到![]() ,
,
故函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
故函数![]() 在
在![]() 时取到最小值,
时取到最小值,
故![]() ;
;
(2)当![]() 时,函数
时,函数![]()
导数为![]() ,
,
若![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
即函数![]() 在区间
在区间![]() ,
,![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增.
上单调递增.
若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
函数![]() 在区间
在区间![]() ,
,![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增.
上单调递增.
综上,若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,无增区间,
,无增区间,
若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,
,![]() ,增区间为
,增区间为![]() ,
,
若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,
,![]() ,增区间为
,增区间为![]() .
.
(3)当![]() 时,设函数
时,设函数![]() .
.
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
![]() ,
,![]() 为增函数,
为增函数,
![]() 在区间
在区间![]() 上递增,
上递增,
∵![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
所以![]() 在
在![]() 上至少有两个不同
上至少有两个不同
的正根![]() ,
,![]() ,
,
令![]() ,求导得,
,求导得, ,
,
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 递增,
递增,![]() ,
,![]() ,
,
当![]() ,
,![]() ,∴
,∴![]() ,
,
当![]() ,
,![]() ,∴
,∴![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() ,∴
,∴![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且直线
上的一个动点,且直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.是否存在点
两点.是否存在点![]() 使得以
使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,说明理由.
的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗![]() 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
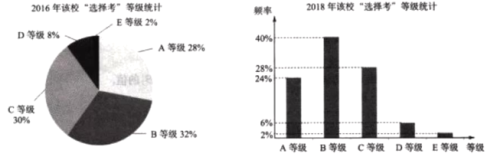
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况如三维饼图(2)所示.对比健身前后,关于这20名肥胖者,下面结论不正确的是( )
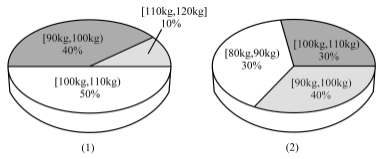
A.他们健身后,体重在区间[90kg,100kg)内的人数不变
B.他们健身后,体重在区间[100kg,110kg)内的人数减少了4人
C.他们健身后,这20位健身者体重的中位数位于[90kg,100kg)
D.他们健身后,原来体重在[110kg,120kg]内的肥胖者体重都至少减轻了10kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局公布的2013-2018年入境游客(单位:万人次)的变化情况,则下列结论错误的是( )
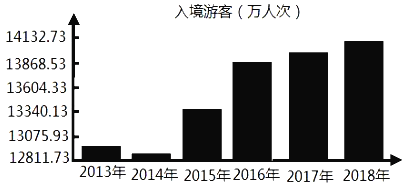
A.2014年我国入境游客万人次最少
B.后4年我国入境游客万人次呈逐渐增加趋势
C.这6年我国入境游客万人次的中位数大于13340万人次
D.前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据历年大学生就业统计资料显示:某大学理工学院学生的就业去向涉及公务员、教师、金融、商贸、公司和自主创业等六大行业.2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业,毕业生人数分别是70人,140人和210人.现采用分层抽样的方法,从该学院毕业生中抽取18人调查学生的就业意向.
(1)应从该学院三个专业的毕业生中分别抽取多少人?
(2)国家鼓励大学生自主创业,在抽取的18人中,含有“自主创业”就业意向的有6人,且就业意向至少有三个行业的学生有7人.为方便统计,将至少有三个行业就业意向的这7名学生分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计如下表:
,统计如下表:
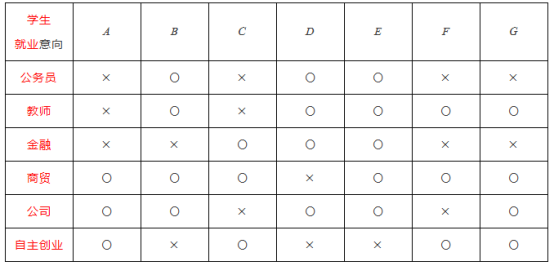
其中“○”表示有该行业就业意向,“×”表示无该行业就业意向.
①试估计该学院2020届毕业生中有自主创业意向的学生人数;
②现从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这7人中随机抽取2人接受采访.设
这7人中随机抽取2人接受采访.设![]() 为事件“抽取的2人中至少有一人有自主创业意向”,求事件
为事件“抽取的2人中至少有一人有自主创业意向”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com