
| A. | $\sqrt{41}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
分析 设点A的坐标为(x1,y1),求出抛物线的准线方程,结合抛物线的定义建立方程关系进行求解即可.
解答 解:设点A的坐标为(x1,y1),抛物线y2=2x的准线方程为x=-$\frac{1}{2}$,
根据抛物线的定义,点A到焦点的距离等于点A到准线的距离,
∵点A到焦点F的距离与其到对称轴的距离之比为5:4,
∴$\frac{{x}_{1}+\frac{1}{2}}{|{y}_{1}|}=\frac{5}{4}$,
∵y12=2x1,
∴解得y1=$\frac{1}{2}$或y1=2,
∵|AF|>2,
∴y1=2,A(2,2).
∴A点到原点的距离为:$\sqrt{4+4}$=2$\sqrt{2}$,
故选:B.
点评 本题主要考查抛物线性质和定义的应用,利用抛物线的定义建立方程关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
 大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.通项公式:an=$\left\{\begin{array}{l}{\frac{{n}^{2}-1}{2},n为奇数}\\{\frac{{n}^{2}}{2},n为偶数}\end{array}\right.$,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( )
大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.通项公式:an=$\left\{\begin{array}{l}{\frac{{n}^{2}-1}{2},n为奇数}\\{\frac{{n}^{2}}{2},n为偶数}\end{array}\right.$,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( )| A. | 1200 | B. | 3612 | C. | 3528 | D. | 1280 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,M是BC的中点,N是CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )
如图,在矩形ABCD中,M是BC的中点,N是CD的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BN}$,则λ+μ=( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
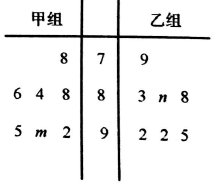 某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )
某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com