已知等比数列{an}a>0,n=1,2,…,且a5•a2n-5=22n(n≥3)则当n>1时,log2a1+log2a3+log2a5+…+log2a2n-1=( )
A.n(2n-1)
B.(n+1)2
C.(n-1)2
D.n2
【答案】
分析:由题意,等比数列{a
n}a>0,n=1,2,…,且a
5•a
2n-5=2
2n(n≥3),又当n>1时,log
2a
1+log
2a
3+log
2a
5+…+log
2a
2n-1=log
2a
1a
3a
5…a
2n-1.由等比数列的性质m+n=s+t,a
ma
n=a
sa
t.求出a
1a
3a
5…a
2n-1的值,即可求出正确答案,得出正确选项
解答:解:由题意等比数列{a
n}a>0,n=1,2,…,
当n>1时,log
2a
1+log
2a
3+log
2a
5+…+log
2a
2n-1=log
2a
1a
3a
5…a
2n-1.
又a
5•a
2n-5=2
2n(n≥3)
∴a
1a
3a
5…a
2n-1=(2
n)
n=
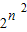
∴log
2a
1+log
2a
3+log
2a
5+…+log
2a
2n-1=log
2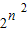
=n
2故选D
点评:本题考查数列与函数的综合,解题的关键是由对数的运算性质进行化简求值,以及由由等比数列的性质求出a
1a
3a
5…a
2n-1值,本题涉及到函数与数列,综合性强,转化灵活,本题主要训练转化的思想,利用性质求值的技能.本题易因为项数求不准而出错,解题时要注意严谨、认真,以防因为运算出错导致解题失败.

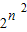
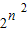 =n2
=n2

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案