
【题目】已知![]() 函数
函数![]()
(1)若关于![]() 的方程
的方程![]() 有两个不同实数根,求
有两个不同实数根,求![]() 的取值范围;
的取值范围;
(2)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据对数相等条件可将方程化为![]() ;令
;令![]() ,
,![]() ,可将方程进一步整理为
,可将方程进一步整理为![]() ;当
;当![]() 时,可验证知不合题意;当
时,可验证知不合题意;当![]() 时,求得
时,求得![]() ,进而得到
,进而得到![]() ;利用
;利用![]() 和对数真数大于零的要求可构造不等式求得结果;
和对数真数大于零的要求可构造不等式求得结果;
(2)根据对数函数单调性可将恒成立的不等式可化为![]() ,利用绝对值不等式的解法可得
,利用绝对值不等式的解法可得![]() 且
且![]() 对
对![]() 恒成立;利用分离变量法将问题转化为
恒成立;利用分离变量法将问题转化为![]() 与函数最值的大小关系,通过求解函数最值得到结果.
与函数最值的大小关系,通过求解函数最值得到结果.
(1)由题意得:![]()
![]()
![]()
整理可得:![]()
设![]() ,
,![]() ,则原方程可化为:
,则原方程可化为:![]()
即:![]()
当![]() ,即
,即![]() 时,原方程可化为
时,原方程可化为![]() ,不存在两个不等实根
,不存在两个不等实根
![]()
![]() 的两根为:
的两根为:![]() ,
,![]()
即![]() ,
,![]()
若原方程有两个不等实根,则![]() ,解得:
,解得:![]() 且
且![]()
又![]() ,
,![]()
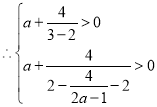 且
且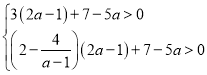 ,解得:
,解得:![]()
![]() 的取值范围为
的取值范围为![]()
(2)由题意得:![]() 对任意
对任意![]() 恒成立
恒成立
![]() ,即
,即![]()
![]()
由![]() 得:
得:![]()
当![]() 时,
时,![]() (当
(当![]() 时取最小值)
时取最小值) ![]()
由![]() 得:
得:![]()
当![]() 时,
时,![]() (当
(当![]() 时取最大值)
时取最大值) ![]() ,即
,即![]()
综上所述:![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了110人,其中女性50人,男性60人.女性中有30人主要的休闲方式是看电视,另外20人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外40人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断性别与休闲方式是否有关系.
下面临界值表供参考:
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式:K2=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“非洲猪瘟”过后,全国生猪价格逐步上涨,某大型养猪企业,欲将达到养殖周期的生猪全部出售,根据去年的销售记录,得到销售生猪的重量的频率分布直方图(如图所示).

(1)根据去年生猪重量的频率分布直方图,估计今年生猪出栏(达到养殖周期)时,生猪重量达不到270斤的概率(以频率代替概率);
(2)若假设该企业今年达到养殖周期的生猪出栏量为5000头,生猪市场价格是30元/斤,试估计该企业本养殖周期的销售收入是多少万元;
(3)若从本养殖周期的生猪中,任意选两头生猪,其重量达到270斤及以上的生猪数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意给定的![]() ,是否存在
,是否存在![]() (
(![]() )使
)使![]() 成等差数列?若存
成等差数列?若存
在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们在求高次方程或超越方程的近似解时常用二分法求解,在实际生活中还有三分法.比如借助天平鉴别假币.有三枚形状大小完全相同的硬币,其中有一假币(质量较轻),把两枚硬币放在天平的两端,若天平平衡,则剩余一枚为假币,若天平不平衡,较轻的一端放的硬币为假币.现有 27 枚这样的硬币,其中有一枚是假币(质量较轻),如果只有一台天平,则一定能找到这枚假币所需要使用天平的最少次数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com